Геометрическое представление булевых функций

Обозначим через 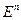множество всех наборов 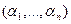, состоящих из чисел ноль и единица. Множество 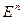называется п-мерным кубом, а набор 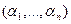- вершинами куба.

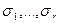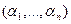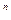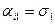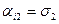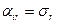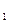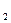Пусть - фиксированный набор чисел из 0 и 1. Множество всех вершин куба Е таких, что , ,…, , 1<i <i <…<i 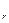,называется (п-r)-мерной гранью. Очевидно, что (n-r)-мерная грань является (n-r)-подкубом куба Е .

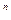Например, в трехмерном кубе Е³ наборы (0, 0, 1) и (0, 0, 0) образуют одномерную ( n=3, r=2) грань ( ребро), а наборы (1, 0, 0), (1, 0, 1), (1, 1, 0), (1,1, 1) - двухмерную грань.

Пусть f( 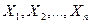) — произвольная булева функция. Ей сопоставляется в соответствие подмножество 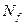вершин куба Е 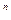, таких что 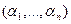Î 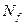тогда и только тогда, когда f 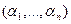=l. Очевидно, что по подмножеству 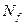исходная функция f( 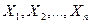) восстанавливается однозначно. Таким образом, геометрический способ задания булевой функции заключается в задании множества вершин п-мерного куба Е 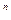, в которых данная функция истинна.

Пример. Пусть функция f( 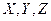) задана таблицей истинности. Составить для нее множество .

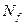x	y	z	f( )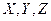

Очевидно, что

N_f={(0,0,1),(0,1,0),(0,1,1),(1,0,0),(1,0,1),(1,1,0)(1,1,1)}. Множество 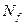можно изобразить следующим образом. Рассмотреть вершины трехмерного куба (или просто куба), каждой вершине поставить в соответствие набор из нулей и единиц. Для этого одну из вершин поместить в начало декартовой системы координат, при этом три вершины должны оказаться на координатных осях. Считая, что ребро куба равно единице, каждой вершине поставим в соответствие набор из нулей и единиц, соответствующий координатам вершины в декартовой системе. Для наглядного изображения геометрического представления булевой функции выделяют вершины куба, в которой функция принимает значение 1. На рис. 5.1 изображено геометрическое представление рассмотренной булевой функции.

Z

Y

X (1,1,0)

Рис. 5.1. Геометрическое представление булевой функции

Для любой булевой функции существует ее представление в СДНФ. Причем в алгоритме построения СДНФ используются только те наборы значений, при которых функция равна единице. Это позволяет проинтерпретировать геометрическое представление функции следующим образом. Рассмотрим, например, ребро куба, представленное вершинами (1,0,0) и (1,0,1), им соответствуют элементарные конъюнкци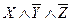и и 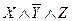. Ребру (одномерному подкубу) соответствует формула .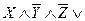

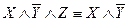Аналогично можно получить формулы, описывающие грани (двумерные подкубы). Например, описанию грани куба, представленной вершинами (1,0,0), (1,0,1), (1,1,0) и (1,1,1), соответствует формула 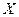. Описанию грани куба, представленной вершинами (0,0,0), (0,0,1), (0,1,0) и (0,1,1), соответствует формула .

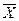Замечание. Для функций, зависящих от четырёх и более переменных, геометрическоепредставление применяется очень редко, т.к. трудно построить наглядную модель n - мерного куба при n>3.

Перейдем теперь к геометрической постановке задачи минимизации булевых функций.