ФУНКЦИИ, ОТОБРАЖЕНИЯ И ОПЕРАЦИИ
Рассмотрим два множества X и Y. Если для каждого элемента 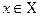 указан элемент
указан элемент 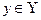 , то говорят, что между множествами X и Y установлено соответствие. Обозначим его через Г. Тогда Г состоит из множества упорядоченных пар (x, y), таких, что
, то говорят, что между множествами X и Y установлено соответствие. Обозначим его через Г. Тогда Г состоит из множества упорядоченных пар (x, y), таких, что 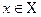 и y
и y 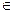 Y : Г
Y : Г 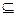
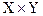 . При этом совершенно необязательно, чтобы в сопоставлении участвовали все элементы множества X и Y.
. При этом совершенно необязательно, чтобы в сопоставлении участвовали все элементы множества X и Y.
Образом элемента x при соответствии Г называется множество Im(x), такое что
Im(x)={y 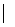 (x,y)
(x,y) 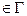 }.
}.
Прообразом элемента y при соответствии Г называется множество
Coim(y)={x 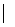 (x,y)
(x,y) 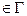 }.
}.
Областью значений соответствия Г называется множество 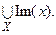
Областью определения соответствия Г называется множество 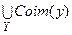 .
.
Для каждого соответствия существует обратное соответствие 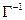 , которое любому y
, которое любому y 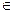 Y сопоставляет x
Y сопоставляет x 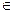 X, причем
X, причем 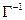 ={(y,x)
={(y,x) 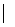 (x,y)
(x,y) 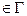 }.
}.
Отображением (однозначным) 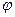 называется такое соответствие, которое каждому х
называется такое соответствие, которое каждому х 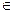 Х сопоставляет единственный элемент у
Х сопоставляет единственный элемент у 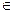 Y . При отображении
Y . При отображении 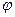 соответствие между х и у записывается в виде у =
соответствие между х и у записывается в виде у = 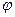 (x), a само отображение определяет запись
(x), a само отображение определяет запись 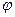 : X
: X 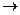 Y, при этом Х называется областью определения отображения, Y – областью значений.
Y, при этом Х называется областью определения отображения, Y – областью значений.
Два отображения 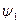 : X
: X 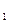
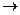 Y
Y 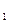 , и
, и 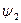 : X
: X 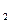
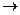 Y
Y 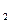 равны, если для всех х
равны, если для всех х 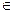 Х, X
Х, X 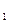 =X
=X 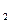 ,Y
,Y 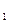 =Y
=Y 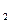 и
и 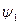 =
= 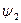 .
.
Отображение называется многозначным, если некоторым значениям х 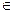 Х соответствуют подмножества Y
Х соответствуют подмножества Y 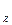
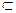 Y, состоящие более чем из одного элемента.
Y, состоящие более чем из одного элемента.
Если Х – область определения, а Y – область значений отображения 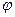 , то говорят, что
, то говорят, что 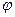 отображает Х на Y. Если
отображает Х на Y. Если 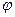 отображает Х на Y и Y
отображает Х на Y и Y 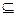 Z , то говорят, что
Z , то говорят, что 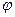 отображает Х в Z.
отображает Х в Z.
Поскольку отображение является частным случаем соответствия, то можно ввести понятие обратного отображения.
Если заданы три множества X, Y, Z и на Х определено отображение f со значениями в Y, а на Y задано отображение g со значениями в Z, то существует отображение h с областью определения в X, принимающее значения в Z и определяемое равенством h(x)=g(f(x)). Это отображение называется композицией отображений g и f или сложным отображением, составленным из внутреннего отображения f и внешнего отображения g.
Рассмотрим некоторые свойства отображений.
Отображение 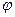 : X
: X 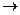 Y называется сюрьективным, или сюръекцией, если любой y
Y называется сюрьективным, или сюръекцией, если любой y 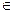 Y есть образ по крайней мере одного х
Y есть образ по крайней мере одного х 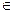 Х. Заметим, что условие
Х. Заметим, что условие 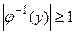 для любого у или |Х|
для любого у или |Х| 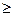 |Y| характеризует сюръекцию.
|Y| характеризует сюръекцию.
Пример. Отображение 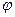 : {1, 2, 3, 4}
: {1, 2, 3, 4} 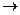 {у
{у 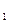 , у
, у 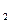 , y
, y 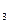 }, такое что
}, такое что 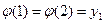 ,
, 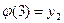 ,
, 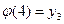 сюръективно. Отображение
сюръективно. Отображение 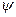 : {1, 2, 3, 4}
: {1, 2, 3, 4} 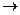 {у
{у 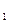 , у
, у 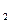 , y
, y 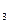 } с условиями
} с условиями 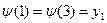 ,
, 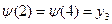 не является сюрьективным.
не является сюрьективным.
Отображение 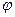 : X
: X 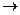 Y называется инъективным, или инъекцией, если каждый элемент y
Y называется инъективным, или инъекцией, если каждый элемент y 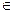 Y имеет хотя бы один прообраз х
Y имеет хотя бы один прообраз х 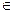 Х либо вообще не имеет прообраза. Можно видеть, что условие
Х либо вообще не имеет прообраза. Можно видеть, что условие 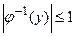 для любого y
для любого y 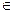 Y или
Y или 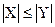 определяют инъекцию.
определяют инъекцию.
Пример. Пусть Х = {1, 2, 3}, Y = {у 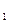 , у
, у 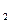 , y
, y 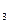 ,
, 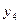 }, Отображение
}, Отображение 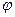 :
: 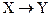 инъективно, если
инъективно, если 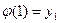 ,
, 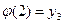 ,
, 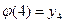 .
.
Если отображение одновременно является сюръективным и инъективным, то оно называется биективным отображением или биекцией. Для биективного отображения 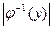 = 1 для любого у или
= 1 для любого у или 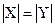 .
.
Пример. 3.3. Пусть Х={1, 2,3}, Y={у 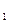 , у
, у 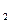 , y
, y 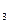 }. Отображение
}. Отображение 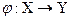 биективно, если
биективно, если 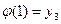 ,
, 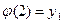 ,
, 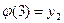 .
.
Биективное отображение определяет взаимно однозначное соответствие между множествами Х и Y. Если между Х и Y можно установить взаимно однозначное соответствие, то множество Х называется эквивалентным множеству Y. Установление взаимно однозначного соответствия между множествами играет важную роль. Так, определение числа элементов конечного множества X, то есть установление равенства 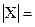 n при некотором n, фактически сводится к отысканию некоторого взаимно однозначного соответствия между множествами Х и N={1,2, ... n}. Множества, равномощные N, называются счетными. Множества равномощны, если между их элементами можно установить взаимно однозначное соответствие, то есть эквивалентные множества являются равномощными.
n при некотором n, фактически сводится к отысканию некоторого взаимно однозначного соответствия между множествами Х и N={1,2, ... n}. Множества, равномощные N, называются счетными. Множества равномощны, если между их элементами можно установить взаимно однозначное соответствие, то есть эквивалентные множества являются равномощными.
Отображение 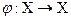 представляет собой отображение самого множества в себя и называется преобразованием множества Х.
представляет собой отображение самого множества в себя и называется преобразованием множества Х.
Пусть f 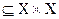 – соответствие между множествами Х и Y. Если для каждого х, такого что (х,у)
– соответствие между множествами Х и Y. Если для каждого х, такого что (х,у) 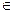 f, имеется единственный образ, то соответствие называется функциональным и определяет функцию f на множестве Х со значениями в множестве Y. Задание функции означает, что определено отображение f:
f, имеется единственный образ, то соответствие называется функциональным и определяет функцию f на множестве Х со значениями в множестве Y. Задание функции означает, что определено отображение f: 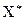
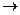 Y, где
Y, где 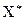
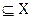 , а для элементов множества
, а для элементов множества 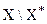 отображение, а значит, и функция f не определены. Значение у в любой из пар (х,у)
отображение, а значит, и функция f не определены. Значение у в любой из пар (х,у) 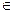 f называется функцией от данного х, что записывается в виде у=f(x).
f называется функцией от данного х, что записывается в виде у=f(x).
На функцию переносятся все рассмотренные свойства отображений, при этом считается, что функция обладает некоторым свойством, если этим свойством обладает соответствующее отображение. Две функции равны, если равны соответствующие им отображения. Функция может быть сюръективной, инъективной или биективной. Функция f, для которой из f(x)=f(y) следует x=у, называется взаимно однозначной. Кроме того, для функции можно ввести понятия обратной функции, композиции функций, которая в этом случае называется суперпозицией.
Примеры. 1.Рассмотрим три функции 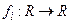 , i=1,2,3:
, i=1,2,3:
1) функция 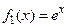 инъективна, но не сюрьективна;
инъективна, но не сюрьективна;
2) функция 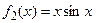 сюрьективна, но не инъективна;
сюрьективна, но не инъективна;
3) функция 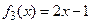 биективна.
биективна.
2. Биекцией между множеством натуральных чисел N и множеством целых чисел Z является функция 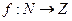 , для которой
, для которой 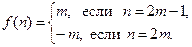
К специальным отображениям относятся понятия оператора и функционала.
Оператор - отображение одного множества на другое, каждое из которых наделено некоторой структурой.
Функционал - отображение произвольного множества Х в множество комплексных или действительных чисел.
Если множество Х в определении функции у=f(x) является декартовым произведением n множеств X 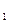 , X
, X 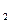 , ..., Xn , то получаем определение n-местной функции у=
, ..., Xn , то получаем определение n-местной функции у= 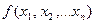
 , Частным случаем n-местной функции является n-местаая операция - n-местная функция, у которой области определения аргументов и область значений совпадают, то есть
, Частным случаем n-местной функции является n-местаая операция - n-местная функция, у которой области определения аргументов и область значений совпадают, то есть 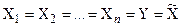 . Таким образом, n-местная операция по n элементам множества Х определяет (n+1)-й элемент этого же множества.
. Таким образом, n-местная операция по n элементам множества Х определяет (n+1)-й элемент этого же множества.
Пример. Сложение, умножение и разность действительных чисел является примерами операций на множестве действительных чисел. Разность двух неотрицательных чисел не является операцией на множестве неотрицательных чисел.
Рассмотрим некоторые свойства бинарных операций.
Операция 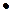 называется
называется
коммутативной, если для любых x, y из множества Х
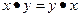 ;
;
ассоциативной, если для любых x, y, z из множества Х
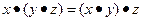 ;
;
дистрибутивной относительно операции 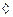 , если для любых x, y, z из множества Х для операций выполняются соотношения
, если для любых x, y, z из множества Х для операций выполняются соотношения
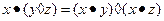 или
или 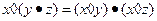 .
.
Замечание. Коммутативность операции означает независимость результата операции от перемены мест аргументов. Ассоциативность означает, что если выражение включает некоторую ассоциативную операцию, то последовательность действий при получении результата может быть произвольной. Известные арифметические операции сложения и умножения чисел являются ассоциативными и коммутативными.
Дата добавления: 2015-04-10; просмотров: 2136;
