Задачи и упражнения
1. Даны множества Х0={1,2,3,4,5,6}, X1={1,2,3,4}, X2={2,3,4,5}, X3={2,3,4}, X4={3,4,5}, X5={2,3}, X6={3,4}, X7={4,5}, X8={2,4}. Сформируйте частичный порядок на этих множествах.
2. Пусть Х - множество всех прямых на плоскости. Являются ли эквивалентными отношения а) параллельности прямых и б) перпендикулярности прямых?
3. Приведите пример четырех различных рефлексивных отношений на множестве 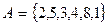 .
.
4. Приведите пример трех различных отношений на множестве 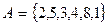 , не являющихся рефлексивными.
, не являющихся рефлексивными.
5. Приведите пример двух различных симметричных отношений и двух различных, не являющихся симметричными, на множестве 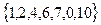 .
.
6. Приведите пример двух различных транзитивных отношений и двух различных, не являющихся транзитивными, на множестве 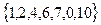 .
.
7. Приведите пример частичного порядка и пример отношения, не являющегося частичным порядком.
8. Приведите пример множества и двух различных эквивалентностей на нем.
9. Приведите пример множества и двух различных частичных порядков на нем.
10. Определите свойства следующих отношений, заданных на множестве действительных чисел (R)
а) R={(x,y)| x,yÎR и x - y<0},
в) R={(x,y)| x,yÎR и 2x ³3y},
с) R={(x,y)| x,yÎR и |x| ³| y|}.
11. Найдите 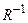 ,
, 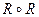 ,
, 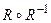 ,
, 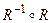 для отношений
для отношений
а) R={(x,y) | x,yÎN и x, делит y},
в) R={(x,y)| x,yÎR и x + y<0},
с) R={(x,y)| x,yÎR и 2x ³3y}.
12. Докажите, что если отношения R1 и R2 рефлексивны, то рефлексивны следующие отношения 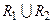 ,
, 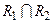 ,
, 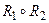 ,
, 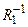 .
.
13. Докажите, что если отношения R1 и R2 симметричны, то симметричны следующие отношения 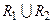 ,
, 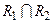 ,
, 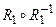 ,
, 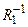 .
.
14. Докажите, что если R эквивалентность, то 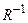 есть также эквивалентность.
есть также эквивалентность.
15. Докажите, что 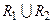 – эквивалентность тогда и только тогда, когда
– эквивалентность тогда и только тогда, когда 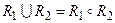 .
.
16. Для отношения, заданного матрицей, определить является ли оно отношением эквивалентности. Если является, то определить классы эквивалентности.
| а) | R | а | b | с | d | е | f | б) | R | а | b | с | d | е | f |
| а | а | ||||||||||||||
| b | b | ||||||||||||||
| с | с | ||||||||||||||
| d | d | ||||||||||||||
| е | е | ||||||||||||||
| f | f |
Дата добавления: 2015-04-10; просмотров: 2807;
