Отношение эквивалентности и разбиения
Введем некоторые специальные типы отношений. Рефлексивное, симметричное, транзитивное отношение называется отношением эквивалентности или эквивалентностью (обозначение I).
Примеры.
1. Отношение равенства на множестве целых чисел R={(x,y)| x,yÎZ и x=y}является отношением эквивалентности, так как оно рефлексивно (x=x), симметрично (x=y 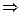 y=x), транзитивно (x=y, y=z
y=x), транзитивно (x=y, y=z 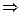 x=z)).
x=z)).
2. Отношение подобия на множестве треугольников являются отношением эквивалентности.
3. Отношение принадлежности к одной студенческой группе на множестве студентов ВГТУ – отношение эквивалентности.
4. Говорят, что целые числа х и у сравнимы по модулю m, если их разность делится на m. Этот факт обозначают в виде х 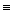 y(mod m). На множестве целых чисел определим бинарное отношение R, полагая xRy, если х
y(mod m). На множестве целых чисел определим бинарное отношение R, полагая xRy, если х 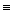 y(mod m). Это отношение называется отношением сравнимости по модулю m. Заметим, что R рефлексивно на множестве целых чисел, так как х-х = 0, и, следовательно, делится на m; R симметрично, так как если (х-у) делится на m, то (у-х) также разделится на т; это отношение транзитивно, так как если (х-у) делится на т, то для некоторого целого t
y(mod m). Это отношение называется отношением сравнимости по модулю m. Заметим, что R рефлексивно на множестве целых чисел, так как х-х = 0, и, следовательно, делится на m; R симметрично, так как если (х-у) делится на m, то (у-х) также разделится на т; это отношение транзитивно, так как если (х-у) делится на т, то для некоторого целого t 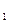 имеем х-у=t
имеем х-у=t 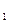 m, а если (y-z) делится на m, то для некоторого целого t
m, а если (y-z) делится на m, то для некоторого целого t 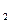 имеем y-z=t
имеем y-z=t 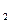 m. Отсюда x-z= =(t
m. Отсюда x-z= =(t 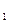 +t
+t 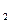 )m, то есть число (x-z) делится на m. Таким образом, отношение сравнимости по модулю m на множестве целых чисел является эквивалентностью.
)m, то есть число (x-z) делится на m. Таким образом, отношение сравнимости по модулю m на множестве целых чисел является эквивалентностью.
Классом эквивалентности K(x) элемента х называется множество всех элементов у 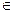 Х, каждый из которых находится с этим элементом в отношении эквивалентности. Иными словами, класс эквивалентности – это множество эквивалентных элементов.
Х, каждый из которых находится с этим элементом в отношении эквивалентности. Иными словами, класс эквивалентности – это множество эквивалентных элементов.
Примеры:
1. Для отношения принадлежности к одной студенческой группе классом эквивалентности является множество студентов одной группы.
2. Отношение сравнимости на множестве целых чисел порождает следующие классы эквивалентности: вместе с любым числом х в этом же классе эквивалентности содержатся все числа вида (у + km), где k – целое число. Очевидно, что числа 0, 1,…, m-1 порождают различные классы эквивалентности, которые называются классами вычетов по модулю m. Все остальные классы эквивалентности для этого отношения совпадают с ними, так как любое число х из множества целых чисел, можно представить в виде
у = tm+ r, где 0 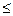 r
r 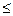 m.
m.
Заметим, что два различных класса эквивалентности не пересекаются, поэтому если все элементы множества Х распределены по классам эквивалентности, то эти классы эквивалентности образуют разбиение множества X. Справедливо утверждение: всякое отношение эквивалентности определяет разбиение множества Х на классы эквивалентности. Множество всех классов эквивалентности называется фактор-множеством по данному отношению эквивалентности и обозначается Х /I.
Пример. Для отношения принадлежности к одной студенческой группе фактор-множество множества студентов ВГТУ представляется собой множество студенческих групп.
Для определения, является ли заданное отношение R отношением эквивалентности используют следующий критерий:
Пусть R – матрица бинарного отношения. Если путем перестановки строк и столбцов ее можно привести к блочно-диагональному виду (на главной диагонали расположены подматрицы, состоящие из 1, а остальные элементы равны 0), то R является отношением эквивалентности, иначе – R не является отношением эквивалентности.
Пример. Рассмотрим отношение R, матрица которого имеет вид
| R | а | b | с | d | е | f |
| а | ||||||
| b | ||||||
| с | ||||||
| d | ||||||
| е | ||||||
| f |
Переставляя строки и столбцы, матрицу отношения R можно привести к блочно-диагональному виду, а значит R является эквивалентностью, и по полученной матрице можно определить классы эквивалентности К 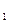 , К
, К 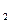 , К
, К 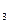 .
.
| R | а | d | b | с | е | f |
| а | ||||||
| d | ||||||
| b | ||||||
| с | ||||||
| е | ||||||
| f |
Таким образом, К 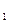 = {а, d), К
= {а, d), К 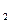 = {b}, К
= {b}, К 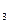 = {с, е, f}.
= {с, е, f}.
Отношение эквивалентности имеет большое практическое значение. Так сущность моделирования заключается в том, что устанавливают отношение эквивалентности между двумя системами, каждая из которых может быль абстрактной или реально существующей. Если одна из систем оказывается проще для исследования, то ее рассматривают в качестве модели для другой. Модель называется изоморфной, если между моделью и реальной системой наблюдается полное поэлементное соответствие (чертеж и изготовленная по нему деталь). Однако часто используются модели, которые позволяют судить только о существенных аспектах поведения реальных систем, не детализируя их (географическая карта по отношению к изображенному на ней участку земной поверхности). Модели, отдельные элементы которых соответствуют лишь крупным частям реальной системы, а полное поэлементное соответствие отсутствует, называются гомоморфными.
Дата добавления: 2015-04-10; просмотров: 2866;
