Отношения порядка. Диаграмма Хассе

Отношение эквивалентности является обобщением отношения равенства: эквивалентные элементы считаются «равными». Обобщением обычного отношения 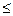служат отношения порядка.

Отношение 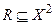называется предпорядком или квазипорядком, если R рефлексивно и транзитивно.

Пример. Отношение

R={(1,1),(2,2),(3,3),(1,2),(2,1),(2,3),(1,3)}

на множестве X={1,2,3} является предпорядком.

Рефлексивное, антисимметричное, транзитивное отношение называется отношением нестрогого порядка и обозначается символом .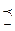

Антирефлексивное, антисимметричное, транзитивное отношение называется отношением строгого порядка и обозначается символом 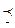. Отношения строгого и нестрогого порядков иначе называют отношениями упорядоченности. Отношение, обратное отношению упорядоченности, также является отношением упорядоченности, т.е. ( ) = .

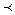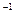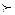Примеры:

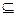
1. Пусть Y – некоторое множество, тогда отношение включения на множестве всех подмножеств P(Y) является отношением нестрогого порядка.

2. Отношение «х старше у» на некотором множестве людей является отношением строгого порядка.

Множество Х с заданным в нем отношением порядка называется упорядоченным этим отношением. Если любые два элемента х и у множества Х находятся между собой в отношении порядка, то множество Х называется линейно упорядоченным или цепью, иначе множество Х называется частично упорядоченным. В частично упорядоченном множестве можно выделить цепь. Цепь с повторяющимися элементами называется мультицепью. Если между элементами х и у установлено отношение порядка, то они называются сравнимыми, иначе – несравнимыми. Антицепью (семейством Шпернера) называется подмножество частично упорядоченного множества, в котором любые два элемента несравнимы. 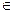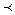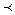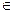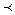Специальным типом частично упорядоченного множества является интервал |x,y]={z X|x z у} (замкнутый) или (x,y)P={z X|x z 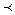у} (открытый).

Двойственным к частично упорядоченному множеству называется частично упорядоченное множество, определенное на том же носителе с помощью обратного отношения. Это понятие лежит в основе принципа двойственности, который часто формулируют в виде: если некоторое утверждение справедливо для частично упорядоченных множеств, то справедливо и двойственное утверждение, то есть утверждение, касающееся двойственных частично упорядоченных множеств.

Рассмотрим множество Х с заданным на нем отношением частичного порядка .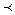

Говорят, что элемент y покрывает элемент x, если х 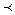у и не существует никакого элемента z 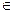X, такого что х 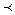z 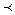у. Таким образом, у покрывает х тогда и только тогда, когда х 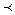у и [х,у]={х,у}. Любое частично упорядоченное множество можно представить в виде схемы. Диаграммой Хассе частично упорядоченного множества Х называ­ется граф, вершинами которого являются элементы множества X, а пара (х,у) образует ребро, если элемент у покрывает элемент х, и такой что, если х 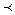у, то у рисуют с большей вертикальной координатой чем х.

Пример. Отношение включения 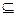на булеане Р(Х), где Х={а, b, с}. Оно является частично упорядоченным множеством. Множество Р(Х) содержит восемь элементов: { 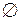, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}}. Диаграмма Хассе для этого отношения будет иметь вид (рис. 2.2).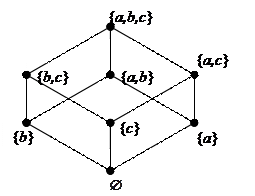

Рис. 2.2

Правило чтения диаграмм Хассе состоит в том, что х у, если можно пройти из точки х в точку у, следуя вдоль восходящих отрезков соединяющих точки. Смена направления движения разрешается только в точках диаграммы.

Пример. Пусть А={1, 2, 3, 5, 6, 10, 15, 30}. Рассмотрим отношение частичного порядка ≤ на этом множестве, задаваемое по правилу: x≤y y делится на x. Диаграмма Хассе изображена на рис.2.3.

Заметим, что диаграммы Хассе этих двух отношений совпадают

Пусть Х и Y два частично упорядоченных множества. Если их диаграммы Хассе совпадают, то эти частично упорядоченные множества имеют одинаковую структуру.

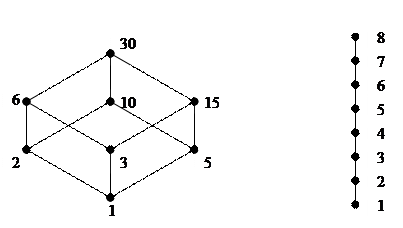Пример. На рис. 2.4 изображена диаграмма Хассе линейно упорядоченного множества Х={1, 2, 3, 4, 5, 6, 7, 8} с обычным отношением порядка (≤) на множестве натуральных чисел, не превосходящих восьми.

Рис. 2.3 Рис. 2.4

Пусть задано частично упорядоченное множество X. Для элементов х и у из множества Х их верхней гранью называется любой элемент z 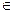Х такой, что 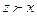и 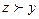, а их нижней гранью – любой элемент t 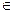X, такой, что 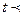х и t 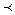у. На языке диаграмм Хассе х 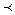у означает, что существует путь из x в y; верхняя грань x и y – это вершина, в которую есть путь из x и y; нижняя грань x и y – это вершина из которой есть путь и в x и в y. В общем случае для некоторых элементов верхняя и нижняя грань может не существовать или быть неединственной, причем различные верхние (или нижние) грани могут быть несравнимы.

Пример. На рис. 2.5 а) изображена диаграмма Хассе множества 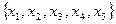, у которого элементы 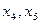не имеют верхней грани, а элементы 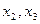– нижней грани. На рис. 2.5 б) изображена диаграмма Хассе множества 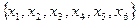у которого все элементы имеют верхние и нижние грани, однако, например, 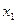и 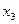имеют две несравнимые верхние грани.

Рис. 2.5