Бинарные отношения. Свойства отношений
Часто при решении задач необходимо выбирать элементы, связанные некоторым соотношением. Примерами таких связей между элементами могут служить функциональные зависимости или отношение «меньше или равно».
В множестве X n-местным или n-арным отношением называется подмножество R n-й декартовой степени 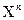 =
= 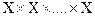 заданного множества,
заданного множества, 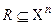 , X называется носителем отношения. Будем говорить, что упорядоченные элементы
, X называется носителем отношения. Будем говорить, что упорядоченные элементы 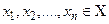 находятся в отношении R, если
находятся в отношении R, если 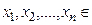 R. Одноместное отношение называется унарным, или свойством, и соответствует подмножеству множества X. Особую роль в приложениях играют бинарные отношения R
R. Одноместное отношение называется унарным, или свойством, и соответствует подмножеству множества X. Особую роль в приложениях играют бинарные отношения R 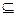 Х
Х 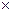 Х. Если
Х. Если 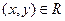 , то пишут также xRy.
, то пишут также xRy.
Пример. Если X={2,3,4,5,6,7,8}, то бинарное отношение R={(x,y)| х делит у и х≤3}, заданное на множестве Х, можно записать в виде R={(2,2), (2,4), (2,6), (2,8), (3,3), (3,6)}.
Рассмотрим отношение R={(x,y)| х≤у, х,у 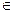 R}, заданное на множестве действительных чисел R. Тогда запись xRy означает, что х≤у, и в качестве имени (обозначения) этого отношения можно взять символ ≤.
R}, заданное на множестве действительных чисел R. Тогда запись xRy означает, что х≤у, и в качестве имени (обозначения) этого отношения можно взять символ ≤.
Каждому бинарному отношению можно поставить в соответствие матрицу бинарного отношения, которую также будем обозначать через R= 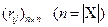 и элементы которой rij определяются следующим правилом:
и элементы которой rij определяются следующим правилом:
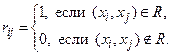
Полученная матрица содержит полную информацию о связях между элементами и позволяет представить эту информацию на компьютере. Заметим, что любая матрица, состоящая из нулей и единиц, является матрицей некоторого бинарного отношения.
Пример. Пусть 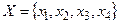 , тогда следующая таблица изображает бинарное отношение
, тогда следующая таблица изображает бинарное отношение
| R | 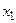
| 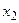
| 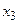
| 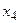
|
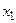
| ||||
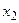
| ||||
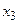
| ||||
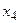
|
Рассмотрим наиболее важные свойства бинарных отношений. Отношение R 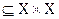 называется
называется
рефлексивным, если для 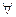 х
х 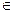 Х (х,х)
Х (х,х) 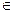 R;
R;
антирефлексивным, если 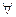 х
х 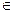 Х (х,х)
Х (х,х) 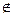 R;
R;
симметричным, если для 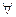 х, у
х, у 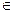 Х ((х,у)
Х ((х,у) 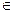 R
R 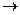 (у,х)
(у,х) 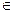 R);
R);
антисимметричным, если для 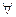 х, у
х, у 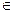 Х ((х,у)
Х ((х,у) 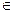 R
R 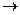 (у,х)
(у,х) 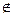 R);
R);
транзитивным, если для 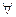 x, у, z ((х,у)
x, у, z ((х,у) 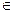 R и (у, z)
R и (у, z) 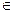 R
R 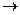 (x,z)
(x,z) 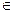 R).
R).
Пример. Следующие отношения, заданные на множестве действительных чисел (R) обладают свойствами рефлексивности, симметричности и транзитивности
R={(x,y)| x,yÎR и x = y},
R={(x,y)| x,yÎR и x2 = y2}.
Отношение R={(x,y)| x,yÎR и x£y}, заданное на множестве действительных чисел, является рефлексивным, так как "х х=х, транзитивным и несимметричным.
Пример. Определим свойства отношения R={(x,y)| x,yÎN и x – делитель y}, заданного на множестве натуральных чисел.
1. Так как 
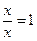 для всех xÎN , то R рефлексивно.
для всех xÎN , то R рефлексивно.
2. Рассмотрим элемент (2,4)ÎR. 2 - делитель 4, но 4 не является делителем 2, т. е. (4,2) 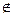 R, следовательно, R - несимметричное отношение.
R, следовательно, R - несимметричное отношение.
3. Так как, если 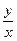 ÎN и
ÎN и 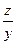 ÎN, то
ÎN, то 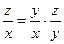 ÎN и R – транзитивно.
ÎN и R – транзитивно.
Матрица бинарного отношения содержит единицы на главной диагонали, если отношение является рефлексивным; такая матрица является симметричной относительно главной диагонали, если отношение симметрично; для антисимметричного отношения произведение элементов, расположенных симметрично относительно главной диагонали, равно нулю.
Пусть на множестве Х задано отношение V 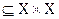 тогда совокупности G = (X,V) называют графом, причем Х – множество вершин графа, а V – множество линий, которые соединяют все или часть из этих вершин. Если в образовании пары (х,у) играет роль порядок элементов, то эту линию называют дугой и изображают направленным отрезком прямой (а граф G называется ориентированным графом или орграфом), иначе – ребром и изображают просто отрезком прямой (граф G в этом случае называется неориентированным графом или неорграфом). Пару противоположно направленных дуг между двумя фиксированными вершинами в графе часто заменяют ребром. Как правило, граф задается с помощью матрицы смежности А={а
тогда совокупности G = (X,V) называют графом, причем Х – множество вершин графа, а V – множество линий, которые соединяют все или часть из этих вершин. Если в образовании пары (х,у) играет роль порядок элементов, то эту линию называют дугой и изображают направленным отрезком прямой (а граф G называется ориентированным графом или орграфом), иначе – ребром и изображают просто отрезком прямой (граф G в этом случае называется неориентированным графом или неорграфом). Пару противоположно направленных дуг между двумя фиксированными вершинами в графе часто заменяют ребром. Как правило, граф задается с помощью матрицы смежности А={а 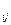 }
} 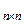 (n=
(n= 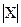 ), элементы которой определяются следующим образом:
), элементы которой определяются следующим образом:
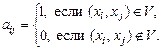
Заметим, что матрица смежности графа совпадает с матрицей соответствующего бинарного отношения.
Пример. Пусть матрица бинарного отношения R, заданного на универсальном множестве U={a,b,c,d,e}, имеет вид
| R | а | b | с | d | е |
| а | |||||
| b | |||||
| c | |||||
| d | |||||
| е |
Тогда соответствующий граф будет иметь вид (рис. 2.1).
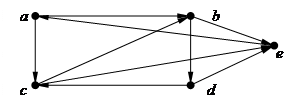 |
Рис. 2.1
Если отношение V рефлексивно, то граф G в каждой вершине имеет петлю; если V симметрично, то любые две вершины графа G соединены парой противоположно направленных дуг; если V антисимметрично, то в G любые две вершины х и у, такие что (х,у) 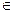 V соединены дугой. В графе G, задающем транзитивное отношение V, для всякой пары дуг, таких что конец первой совпадает с началом второй, существует третья дуга, имеющая общее начало с первой и общий конец со второй – транзитивно замыкающая дуга.
V соединены дугой. В графе G, задающем транзитивное отношение V, для всякой пары дуг, таких что конец первой совпадает с началом второй, существует третья дуга, имеющая общее начало с первой и общий конец со второй – транзитивно замыкающая дуга.
Так как отношение является прежде всего множеством упорядоченных пар, то для отношений можно ввести те же операции, что и для множеств, то есть операции объединения, пересечения, разности и дополнения. Кроме того, для отношений существуют специальные операции:
инверсией отношения R (или обратным к отношению R) называется отношение 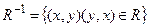 . Матрица обратного отношения
. Матрица обратного отношения 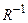 равна транспонированной матрице отношения R:
равна транспонированной матрице отношения R: 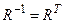 .
.
Пусть 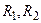 – отношения, заданные на множестве X, тогда композицией отношений R
– отношения, заданные на множестве X, тогда композицией отношений R 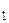 и R
и R 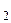 называется отношение, определяемое следующим образом:
называется отношение, определяемое следующим образом:
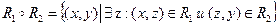
Заметим, что 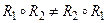 .
.
Замечание. Операция композиции позволяет определить свойство транзитивности. Если выполняется включение 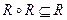 , то отношение транзитивно.
, то отношение транзитивно.
Утверждение 2.1.1. Для любых бинарных отношений Р, Q, R выполняются следующие свойства:
1) 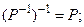
2) 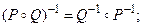
3) 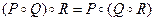 (ассоциативность композиции).
(ассоциативность композиции).
Доказательство. 1. По определению обратного отношения условие 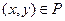 равносильно условию
равносильно условию 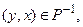 что в свою очередь выполняется тогда и только тогда, когда
что в свою очередь выполняется тогда и только тогда, когда 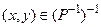 . Следовательно,
. Следовательно, 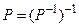 .
.
2. Предположим, что 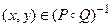 . Тогда
. Тогда 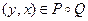 , и, следовательно,
, и, следовательно, 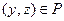 и
и 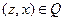 для некоторого элемента z. Значит,
для некоторого элемента z. Значит, 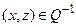 ,
, 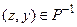 и
и 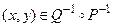 . Включение
. Включение 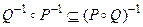 доказывается аналогично.
доказывается аналогично.
3. Пусть 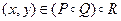 . Тогда для некоторых u и v имеем
. Тогда для некоторых u и v имеем 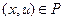 ,
, 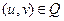 ,
, 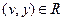 . Таким образом,
. Таким образом, 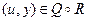 и
и 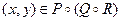 . Включение
. Включение 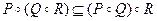 доказывается аналогично.
доказывается аналогично.
Дата добавления: 2015-04-10; просмотров: 7634;
