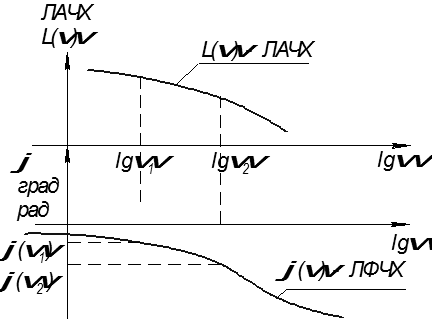
Логарифмические частотные характеристики.

ЛЧХ - зависимость относительной амплитуды колебаний и фазового сдвига от частоты, построенная в логарифмических или полулогарифмических координатах.

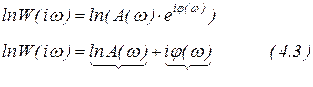
L(ω)=20 · lgA(ω) (4.4)

Для практических расчетов особенно широко используют частотные характеристики, построенные в логарифмическом масштабе в виде ломанных линий из прямолинейных отрезков. Логарифмируя выражение 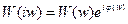, получим

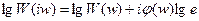
Логарифмической единицей усиления или ослабления мощности сигнала при прохождении его через какое-либо устройство при выражении десятичным логарифмом значение отношения мощности на выходе Рвых к мощности на входе Рвх в технике принят бел. Так как мощность сигнала пропорциональна квадрату его амплитуды, то с учетом

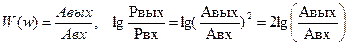
Так как бел является достаточно крупной единицей усиления (ослабления) мощности, то в ТАУ за единицу усиления принят децибел 1 дБ = 0,1 Б. С учетом этого

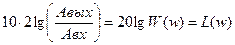Величину логарифма АФЧХ, выраженную в децибелах 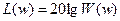называют ЛАЧХ.

Фазочастотную характеристику φ(w) построенную в логарифмических координатах называют ЛФЧХ.

За единицу частоты принята логарифмическая единица – октава или более крупная декада. Октавой называют диапазон частот между какой-либо частотой и ее удвоенным значением. В логарифмическом масштабе частот отрезок в одну октаву имеет одну и туже длину, не зависит от величины частоты и равен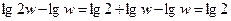

Декадой называют интервал частот между какой-либо величиной частоты и ее десятичным значением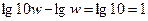

[L] дБ децибелы

декады

октава единицы измерения по оси частот

Декада - отрезок, который соответствует десятикратному изменению частоты

Октава - отрезок, который соответствует двукратному изменению частоты

ЛФЧХ - зависимость фазового сдвига 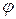от десятичного логарифма частоты.

Частоты на этих графиках наносят в логарифмическом масштабе, а указывают натуральное значение.

Применение логарифмического масштаба удобно возможностью показать широкий диапазон изменения частот. С помощью этих характеристик можно оценить ряд важных показателей, которые характеризуют устойчивость и качество системы.