Временные и частотные характеристики
Динамические свойства линейных звеньев и САУ в целом могут быть представлены помимо уравнений временными и частотными характеристиками.
Эти характеристики могут быть сняты 1) экспериментально или построены 2) по уравнению звена.
Временные и частотные характеристики однозначно связаны с уравнениями звеньев (и систем) и наряду с ними являются исчерпывающим описанием динамических свойств звеньев (и САУ в целом).
Переходная и весовая функции
Временные характеристики – это реакция звена на типовой сигнал. В ТАУ используют две временные характеристики:
1) переходная функция (характеристика)
2) весовая функция (характеристика)
Переходная характеристикаh(t) представляет собой переходный процесс на выходе звена, возникающий при подаче на его вход единичного скачкообразного воздействия (единичная ступенчатая функция).
 |
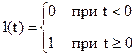
|
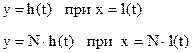
Ступенчатая функция представляет собой распространенный сигнал в автоматических системах:
- мгновенное изменение нагрузки (Мс);
- мгновенное изменение напряжения сети (Uс);
- мгновенное изменение входного воздействия (особенно при логическом управлении).
Ступенчатую функцию (сигнал) легко реализовать при экспериментальных исследованиях (тумблер, резкий поворот потенциометра и т.п.).
Переходную характеристику h(t) можно получить аналитически – это решение дифференциального уравнения системы (звена) при х = 1(t) → обычно для анализа показателей.
Функция веса w(t) – реакция звена на единичный импульс → дельта-функцию Дирака.
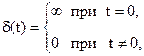
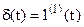 .
.
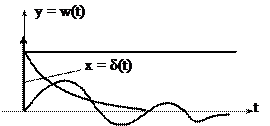 Дельта-функция – математическая идеализация предельно короткого импульса с единичной площадью
Дельта-функция – математическая идеализация предельно короткого импульса с единичной площадью 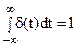 .
.
На практике δ(t) это:
- "удар" (на валу, в насосе лопасть корабля);
- ток "к.з." в электромеханических системах (нарастание и мгновенное отключение с помощью предохранителя)
- "взрыв".
Вследствие принципа суперпозиции имеем:
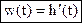 и
и 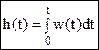 .
.
Общий вывод: 1) В отличие от математики в инженерной практике значительно чаще в качестве временной характеристики используют переходную функцию, т.к. она реализуема в отличие от δ(t), который реализуется только приближенно.
2) Более того, зная h(t) можно определить и 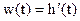 .
.
3) В ТАУ h(t) используется для оценки качества системы.
Следует заметить, что весовая и переходная характеристики связаны с передаточной функцией следующими преобразованиями:
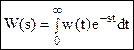 - преобразование Лапласа (вход δ(t) → 1),
- преобразование Лапласа (вход δ(t) → 1),
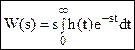 - преобразование Карсона (вход = 1 (t) → 1).
- преобразование Карсона (вход = 1 (t) → 1).
Отсюда следует, что преобразование Карсона больше подходит для инженера.
Примечание: По большому счету (в общем) ПФ – это отношение изображений выходного сигнала ко входному. Но по Карсону 1 (t) → 1, а по Лапласу δ(t) = 1.
Частотные характеристики
Частотные характеристики описывают установившиеся вынужденные колебания на выходе звена при подаче на его вход гармонического воздействия
 |
Здесь X, Y – амплитуды входного и выходного сигнала; ω – круговая частота (ω = 2πf); φ – фазовый сдвиг (угол).
В установившемся режиме (т.е. после окончания переходного процесса) на выходе будут существовать гармонические колебания с частотой ω, но отличающиеся амплитудой и фазой. Чем выше частоты обычно за счет инерционных свойств звена (системы) амплитуда уменьшается, а фаза увеличивается (до определенного предела).
Поэтому относительное изменение амплитуды от частоты 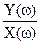 и фазы от ω – φ(ω) были введены как основные частотные характеристики:
и фазы от ω – φ(ω) были введены как основные частотные характеристики:
АЧХ: 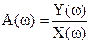 - амплитудная частотная характеристика,
- амплитудная частотная характеристика,
ФЧХ: φ (ω)– фазовая частотная характеристика.
Примерный вид у обычных инерционных (динамических) звеньев.
 | |||
 | |||
АЧХ в силу инерционности по мере увеличения ω спадает до нуля. Чем больше инерционность звена (САУ), тем уже полоса пропускания.
Теоретически АЧХ продолжается до бесконечности, но практически полоса пропускания оценивается до уровня 5% от А(0).
Задача. Как получить аналитически выражения для А(ω) и φ(ω)?
Решение: На основе примера ЭД п.т.н.в. – дифференциальное уравнение 2-го порядка
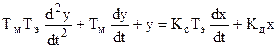 , (1)
, (1)
где у = Ω, х = Мс – такое обозначение удобнее для вывода (проще запись).
При гармоническом сигнале вход x(t) равен:
x=Xejωt
тогда
y=Yej(ωt+φ),
а производные будут иметь вид:
x(n)=(jω)nXejωt
y(k)=(jω)kYej(ωt+φ)
Подставим все это в исходное уравнение, тогда
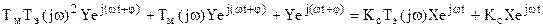 /
/
Сократим обе части на еjωt, тогда после преобразования получим:
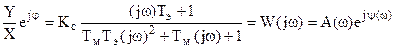 (2)
(2)
Это выражение называется частотной передаточной функцией W(jω), которая являясь функцией комплексного переменного представляется как
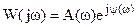 (3)
(3)
сравнивая (2) и (3) получим
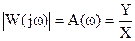 ,
, 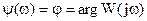
Если сравнить W(jω) с 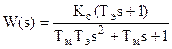 можно сделать вывод (правило):
можно сделать вывод (правило):
Для получения частотной передаточной функции на основе ПФ W(s) необходимо в последней сделать замену s = jω.
Решая аналогичные примеры, или в общем виде через преобразование Фурье (s = jω) получим тоже правило.
Примечание: Частная ПФ – есть преобразование Фурье функции веса, т.е. имеет место интегральное преобразование
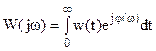 .
.
Частотная ПФ может быть представлена в виде
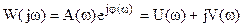 ,
,
где A(ω) – модуль, φ(ω) – аргумент (фаза),
U(ω), V(ω) – вещественная и мнимая частотные характеристики (ВЧХ и МЧХ).
А(ω) определяется как отношение модулей числителя и знаменателя ЧПФ, а фаза φ(ω) – как разность аргументов числителя и знаменателя.
Например: 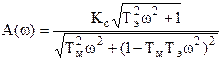
Правило получения модуля: умножение на сопряженное комплексное число и извлечение корня, т.е. как гипотенуза по Пифагору: 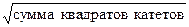 .
.
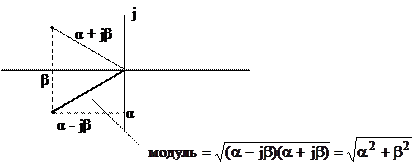 |
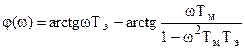
Правило определения фаз: arctg отношения мнимой части комплексного числа к вещественной.
Частотные характеристики удобно изображать графически в виде годографа амплитудно-фазовой характеристики (АФХ):
Методика построения:
1) строится таблица
 |
| ω | А(ω) | φ(ω) | U(ω) | V(ω) |
| ω1 | А(ω1) | φ(ω1) | U(ω1) | V(ω1) |
| ω2 | А(ω2) | φ(ω2) | U(ω2) | V(ω2) |
2) для разных частот рассчитываются А(ωi), φ(ωi)
3) вычисляются U(ωi) и V(ωi) по формулам (так удобнее и точнее):
U(ωi) = A(ωi) cosωit
V(ωi) = A(ωi) sinωit
4) на комплексную плоскость наносятся точки [U(ωi), V(ωi)] для каждой ωi и соединяются плавной кривой.
Для построения частотных характеристик удобнее использовать логарифмический масштаб, т.к. значительно упрощается построение А(ω) – по существу для этого используется кусочно-ломаная линия.
Примечание: U(ω) и V(ω) в ТАУ редко определяют по правилу выделения в W(jω) вещественной и мнимой составляющих, т.к. процедура весьма затруднительна.
| <== предыдущая лекция | | | следующая лекция ==> |
| Классификация минералов по происхождению | | | Происхождение и классификация горных пород |
Дата добавления: 2015-06-27; просмотров: 6867;
