Метод наименьших квадратов

Этот метод наиболее часто используется для получения уравнения регрессии. Предположим, между значениями х и у существует линейная зависимость у=а+bх.

Нам нужно найти такую функцию y*=f(x)=a*+b*x - которая проходила бы как можно ближе к функции у.

Будем искать такую функцию f(x), для которой величина

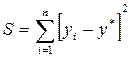
была бы минимальной. Это метод наименьших квадратов. Итак, ищем минимум функции:

S = (y_i-a^*-b^*×x_i)²

Для этого нужно взять частные производные функции S по а^* и по b* 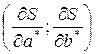, приравнять их к нулю и решить полученную систему уравнений.

Получим

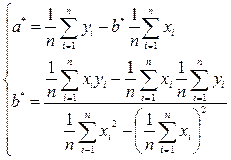
Имея уравнение у^*=a^*+b^*x и подставляя в него значения x за будущий период, можно осуществить прогнозирование.