Решение задачи
Определение вектора конечной продукции за предыдущий период
По условию задачи известны объемы производства каждой из отраслей за предыдущий период (суммарный выпуск продукции отрасли i): X1=600, Х2=1000, Х3= 800 и значения xij (i,j = 1, 2, 3):
х11=250; х12=100; х13=160
х21=150; х22=500; х23=0;
х31=0; х32=300; х33=400.
Отсюда, используя, можно определить значения Yi, i=1,2,3 конечной продукции каждой из отраслей за предыдущий период.
Y1 =600-250-100-160=90;
Y2 =1000-150-500-0=350;
Y3 =800-0-300-400=100.
Таким образом, вектор конечной продукции за предыдущий период найден:
Yn = 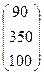
Для определения вектора выпуска продукции X при заданном конечном прогнозируемом векторе спроса Y = 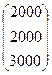 надо решить систему уравнений, из которой следует, что
надо решить систему уравнений, из которой следует, что
X=(Е-А)-1Y
где Е - единичная матрица
Е = 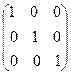
S=(E-A)-1 - называется матрицей полных затрат.
Определение коэффициентов прямых затрат
Учитывая, что технология производства не изменилась, определим коэффициенты прямых затрат aij.
a11=250/600=0,417; a12=100/1000=0,1; a13=160/800=0,2
a21=150/600=0,25; a22=500/1000=0,5; a23=0/800=0;
a31=0/600=0; a32=300/1000=0,3; a33=400/800=0,5.
Таким образом, матрица коэффициентов прямых затрат будет иметь вид
А = 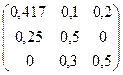
Проверка продуктивности матрицы
Все элементы матрицы А неотрицательные, А≥0.
Для того чтобы система уравнений имела единственное неотрицательное решение при любом неотрицательном векторе Y, необходимо, чтобы матрица А была продуктивной. Экономический смысл продуктивности состоит в том, что существует такой план выпуска продукции, при котором каждая отрасль сможет произвести некоторое количество конечной продукции. Известно, что для продуктивности матрицы А≥0 необходимо и достаточно, чтобы все главные миноры матрицы (Е-А) были положительными числами, строго меньше единицы. Кроме того, если сумма элементов каждого из столбцов неотрицательной квадратной матрицы положительна и строго меньше единицы, то все главные миноры матрицы (Е-А) положительны и строго меньше единицы.
Суммы элементов каждого столбца матрицы А соответственно равны:
0,417 + 0,25 + 0 = 0,667;
0,1 + 0,5 + 0,3 = 0,9;
0,2 + 0 + 0,5 = 0,7.
Следовательно, в силу вышесказанного, матрица А продуктивна, выражение X=(Е-А)-1Y имеет смысл и вектор Y неотрицателен. Следовательно, для нахождения плана выпуска продукции Xможно воспользоваться формулой X=(Е-А)-1Y.
Вычисление матрицы Е-А
Вычислим матрицу (Е-А):
E-A =  -
- 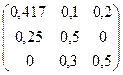 =
= 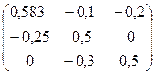
Вычисление обратной матрицы (Е-А)-1
Известно, что матрица В-1 называется обратной по отношению к квадратной матрице В, если произведение В×В-1=Е (Е - единичная матрица).
Для вычисления обратной матрицы воспользуемся формулой:
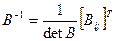
Здесь [Bij] - матрица, полученная из элементов Bij, a Bij - алгебраические дополнения элементов ij матрицы.
Вij=(-1) i+jMij
где Мij - минор элемента Bij (минор - это такой определитель, который получается из матрицы вычеркиванием строки и столбца, на пересечении которых стоит данный элемент).
Вычислим значения алгебраических дополнений элементов матрицы (Е-А). Обозначим для простоты описания вычислений Е-А=В:
B11 = (-1)1+1  = 0,25
= 0,25
B12 = (-1)1+2 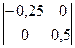 = 0,125
= 0,125
B13 = (-1)1+3 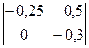 = 0,075
= 0,075
B21 = (-1)2+1  = 0,11
= 0,11
B22 = (-1)2+2 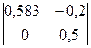 = 0,292
= 0,292
B23 = (-1)2+3 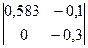 = 0,075
= 0,075
B31 = (-1)3+1 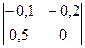 = 0,1
= 0,1
B32 = (-1)3+2 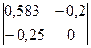 = 0,05
= 0,05
B33 = (-1)3+3 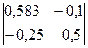 = 0,267
= 0,267
Таким образом, [E-A] = [Bij] = 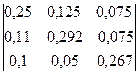
Вычисление транспонированной матрицы
Поменяв в матрице [Е-А] строки и столбцы местами, получаем:
[E-A]T = [Bij] T= 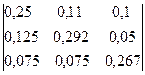
Вычисление определителя матрицы [Е-А]
Вычислим определитель, применив разложение по первой строке
det(Е-А)= 0,583× 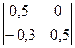 - (-0,1)×
- (-0,1)× 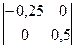 - (-0,2)×
- (-0,2)× 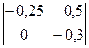 = 0,018
= 0,018
Вычисление матрицы прямых затрат S
По формуле S=(E-A)-1 = 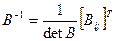 =
= 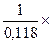
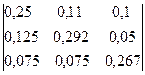 =
=
= 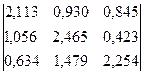
Определение вектора выпуска продукции X
Зная S и Y, вычислим Х по формуле:
Х = S×Y = 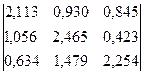 ×
× 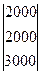
Отсюда
Х1 = 2,113 × 2000 + 0,93 × 2000 + 0,845 × 3000 = 8620;
Х2 = 1,056 × 2000 + 2,465 × 2000 + 0,423 × 3000 = 8310;
Х3 = 0,634 × 2000 + 1,479 × 2000 + 2,254 × 3000 = 10986.
Таким образом, вектор выпуска продукции в следующем периоде при заданном векторе конечной продукции
Yc = 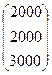 Х =
Х = 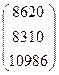
Очевидно, что с использованием матричных операций в Excel процедура вычислений в балансовой модели существенно упростится.
Реализация балансовой модели в электронной таблице Excel показана в табл. 4.2.2 (режим показа формул) и в табл. 4.2.3 (режим вычислений).
Таблица 4.2.2
| A | B | C | D | |
| БАЛАНСОВАЯ МОДЕЛЬ | ||||
| Объём производства | Потребление отраслей | |||
| Вычисление технологических коэффициентов | =B3/A$3 | =C3/A$4 | =D3/A$5 | |
| =B4/A$3 | =C4/A$4 | =D4/A$5 | ||
| =B5/A$3 | =C5/A$4 | =D5/A$5 | ||
| Проверка продуктивности матрицы А | ||||
| =СУММ(B6:B8) | =СУММ(C6:C8) | =СУММ(D6:D8) | ||
| =ИЛИ(B10>=1;C10>=1;D10>=1) | =ЕСЛИ(A11="ИСТИНА";"Решения нет"; "Матрица продуктивна") | |||
| Единичная матрица | ||||
| Вычисление Е-А | =B12-B6 | =C12-C6 | =D12-D6 | |
| =B13-B7 | =C13-C7 | =D13-D7 | ||
| =B14-B8 | =C14-C8 | =D14-D8 | ||
| Вычисление обратной матрицы | =МОБР(B15:D17) | =МОБР(B15:D17) | =МОБР(B15:D17) | |
| =МОБР(B15:D17) | =МОБР(B15:D17) | =МОБР(B15:D17) | ||
| =МОБР(B15:D17) | =МОБР(B15:D17) | =МОБР(B15:D17) | ||
| Спрос на будущий период | План выпуска продукции | =МУМНОЖ(B18:D20;B21:B23) | ||
| =МУМНОЖ(B18:D20;B21:B23) | ||||
| =МУМНОЖ(B18:D20;B21:B23) |
В строке 11 размещены формулы для проверки продуктивности матрицы технологических коэффициентов.
В ячейке А11 формула
=ИЛИ(B10>=l;C10>=l;D10>=l)
проверяет содержимое ячеек B10:D10. Если хотя бы в одной из этих ячеек значение больше единицы (т.е. сумма значений элементов хотя бы в одном столбце превышает единицу), то в ячейку А11 будет записано значение «ИСТИНА». В противном случае - значение «ЛОЖЬ»;
В ячейку С11 введена формула
=ЕСЛИ(А11="ИСТИНА";"Нет решения";"Матрица продуктивна")
Эта формула проверяет содержимое ячейки А11 и если сумма элементов хотя бы одного столбца превысила единицу, выводит сообщение "Нет решения", в противном случае - "Матрица продуктивна".
Таблица 4.2.3
| А | В | С | D | |
| БАЛАНСОВАЯ МОДЕЛЬ | ||||
| Объём производства | Потребление отраслей | |||
| Вычисление технологических коэффициентов | 0,417 | 0,1 | 0,2 | |
| 0,25 | 0,5 | |||
| 0,3 | 0,5 | |||
| Проверка продуктивности матрицы А | ||||
| 0,667 | 0,900 | 0,700 | ||
| ЛОЖЬ | Матрица продуктивна | |||
| Единичная матрица | ||||
| Вычисление Е-А | 0,583 | -0,1 | -0,2 | |
| -0,25 | 0,5 | |||
| -0,3 | 0,5 | |||
| Вычисление обратной матрицы | 2,113 | 0,930 | 0,845 | |
| 1,056 | 2,465 | 0,423 | ||
| 0,634 | 1,479 | 2,254 | ||
| Спрос на будущий период | План выпуска продукции | 8619,72 | ||
| 8309,86 | ||||
| 10985,92 |
Дата добавления: 2015-01-13; просмотров: 1355;
