Математическая постановка задачи
Для решения поставленной задачи можно использовать балансовую модель Леонтьева. Она представляет собой систему уравнений, каждое из которых выражает требование равенства (баланса) между количеством продукции, производимой отдельным экономическим объектом, и совокупной потребностью в этой продукции. В рассматриваемой задаче экономическая система состоит из трех отраслей.
Пусть Хi — величина, равная суммарному выпуску продукции отрасли i;
Хij - количество продукции отрасли i, необходимое для того, чтобы отрасль j произвела Хj единиц своей продукции;
Yj - количество продукции отрасли i, оставшейся для внешнего потребления (конечная продукция).
Тогда взаимосвязь отраслей в процессе производства и потребления отдельного продукта Xi (i= 1, 2, 3) может быть описана в виде следующих уравнений:
Х1 = х11+х12+х13+Y1;
Х2 = х21+х22+х23+Y2;
Х3 = х31+х32+х33+Y3.
Используем понятие коэффициентов прямых затрат (технологических коэффициентов) аij:
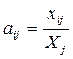 - количество продукции отрасли i, необходимое для того, чтобы отрасль j произвела одну единицу своей продукции.
- количество продукции отрасли i, необходимое для того, чтобы отрасль j произвела одну единицу своей продукции.
Тогда xij=aijXj и система уравнений будет иметь следующий вид:
Х1 = a11X1+a12X2+a13X3+Y1;
Х2 = a21X1+a22X2+a23X3+Y2;
Х3 = a31X1+a32X2+a33X3+Y3.
Или в матричной форме
X=AX+Y,
где A = 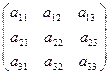 - матрица прямых затрат;
- матрица прямых затрат;
Х- вектор-столбец выпуска продукции в предыдущем периоде X = 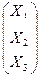 ;
;
Y - вектор-столбец конечного спроса в предыдущем периоде Yc = 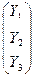
Решим уравнение X=AX+Y относительно X:
X-AX=Y,
отсюда,
Х(Е-А)=Y,
где Е - единичная матрица. Из уравнения получаем X=(Е-А)-1Y
Дата добавления: 2015-01-13; просмотров: 868;
