При Q < 0 (2) — втекание жидкости в начало координат — сток. В первом случае в бесконечно удаленной точке имеем источник, а во втором — сток.
Вычислим объем жидкости, протекающей за единицу времени через поверхность сферы S некоторого радиуса r с центром в начале координат. Через элемент сферы ds за единицу времени протекает объем жидкости v ds, а через всю сферу
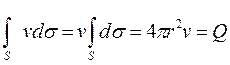 (расход жидкости)
(расход жидкости)
( v можно вынести за знак интеграла, так как v = const на поверхности сферы). Заметим, что первые два равенства верны всегда, когда v = v (r) и v ортогональна к поверхности сферы S. Вычисленный объем жидкости не зависит от r. Таким образом, несмотря на то, что на разных сферах разного радиуса с центром в начале координат скорости разные, постоянная Q в потенциале j (1.42) является объемом жидкости протекающей за единицу времени через каждую такую сферу. Величина Q называется расходом или мощностью источника (стока).
Если Q = const, то источник или сток имеет постоянную мощность;если Q = Q (t) — то переменную. Если в некоторый момент времени Q меняется в начале координат, то мгновенно измеряется поле скоростей во всем пространстве. Сигналы изменение Q сразу сказываются на всем поле скоростей, что, конечно, не может иметь места в действительности. Возмущения должны распространяться с некоторой конечной скоростью. Поэтому рассмотренное поле скоростей является определенной идеализацией, которая может достаточно хорошо отражать действительность только в том случае, когда рассматриваются течения жидкости с большой скоростью распространения возмущений. Во многих случаях можно считать, что такой жидкостью является, например, вода, в которой скорость распространения слабых возмущений 1450 м/сек.
Греческий алфавит 
Α α – альфа Ν ν – ни (ню)
Β β – бэта Ξ ξ – кси 
Γ γ – гамма Ο ο – омикрон
Δ δ – дельта Π π – пи
Ε ε – эпсилон Ρ ρ – ро
Ζ ζ – дзэза Σ σ – сигма
Η η – эта Τ τ – тау
Θ θ – тэта Υ υ – ипсилон
Ι ι – иота Φ φ – фи
Κ κ – каппа Χ χ – хи
Λ λ – ламбда Ψ ψ – пси
Μ μ – ми (мю) Ω ω – омега
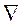 - набла (от греч.-ναβλα - арфа) – знак действия над полем (оператор) –
- набла (от греч.-ναβλα - арфа) – знак действия над полем (оператор) –
этот оператор Гамильтона векторно-дифференциальный
Дата добавления: 2015-03-07; просмотров: 941;
