Тогда закон сохранения массы т принимает вид

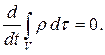(2.1)

Здесь не только плотность ρ — функция от координат точек пространства и времени, но и объем V зависит от t. Принимая это во внимание при вычислении производной в равенстве (2.1), несложно получить равенство

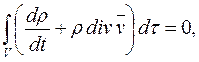
и так как оно справедливо для любого индивидуального объема, то получим первое основное дифференциальное уравнение механики сплошной среды

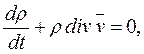(2.2)

которое называется уравнением неразрывности в переменных Эйлера. Это уравнение накладывает ограничение на скорость точек сплошной среды и применяется при больших перемещениях точек среды.

Если воспользоваться формулой (1.5), то уравнение (2.2) можно переписать в виде

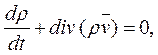(2.3)

В цилиндрической системе координат (r, Θ, z) при осевой симметрии 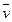= 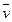(r, z) уравнение неразрывности принимает вид

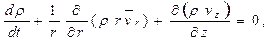
Интересно, что уравнение (2.3) легко получить сразу, остава­ясь строго на точке зрения Эйлера. Для этого достаточно рассмотреть поток вектора ρ 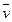сквозь некоторую неподвижную замкнутую поверхность S произвольной формы. Нам известно [см. формулу (1.10)], что этот поток может быть представлен в виде

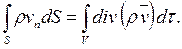
Он выражает массу среды, вытекающую за единицу времени из замкнутой поверхности S. Так как это повлечет за собой уменьшение плотности внутри S в единицу времени, равное (- dρ/dt), и соответственно изменение массы среды внутри S, равное

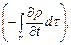то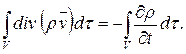

Отсюда следует уравнение (2.3).