Для несжимаемой жидкости dρ/dt (хотя ∂ρ/∂t≠0), уравнение неразрывности (2.2) приобретает вид
div 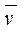 =
= 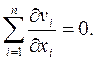
В этом случае поток скорости через любую неподвижную замкнутую поверхность равен нулю, т. е. объем втекающей жидкости равен объему вытекающей. Применяя это свойство к замкнутой поверхности, образованной трубкой тока и ее нормальными сечениями, получим
v1S1=v2S2 .
Конечно, не существует сред, в строгом смысле действительно несжимаемых, однако весьма часто в инженерной практике предположение о постоянстве ρ приводит к значительному упрощению задачи и почти не вносит ошибки.
Для стационарных движений ∂ρ/∂t = O, уравнение неразрывности получает вид
div ρ 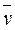 = 0или
= 0или 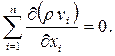
Уравнение (2.2) или (2.3) справедливо для любой однородной сплошной среды, когда нет поглощений массы, химических реакций, внутренней диффузии и других процессов, связанных с влиянием окружающих тел. Однако оно легко обобщается для многокомпонентных смесей или многофазных сред с учетом различного взаимного влияния компонентов (или фаз).
Для этого всякий индивидуальный объем можно представить как совокупность п континуумов, каждый из которых имеет свою плотность ρ1, ρ2, ..., ρn и свою скорость 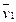 ,
, 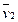 , …,
, …, 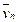 . Если в смеси не происходит химических реакций и других процессов взаимных превращений, то для каждого компонента смеси должен выполняться закон сохранения массы
. Если в смеси не происходит химических реакций и других процессов взаимных превращений, то для каждого компонента смеси должен выполняться закон сохранения массы
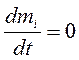 или
или 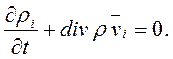
Если же в смеси происходят химические реакции, то массы компонентов тi могут меняться. Пусть γi — изменение массы тi i-го компонента смеси в единицу времени на единицу объема за счет химической реакции. Тогда уравнение неразрывности для компонента смеси можно записать в виде
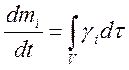 или
или 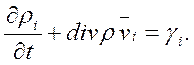 (2.4)
(2.4)
Дата добавления: 2015-03-07; просмотров: 1297;
