ИСТОЧНИК И ИСТОК В ПРОСТРАНСТВЕ
Рассмотрим еще один важный для дальнейшего пример потенциального течения. Пусть
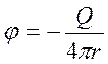 (1.42)
(1.42)
где 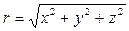 , a Q = const или Q = Q (t). Ясно, что поверхностями равного потенциала j = const являются в этом случае поверхности r = const, т. е. концентрические сферы с центром в начале координат. Скорость v = grad j ортогональна к этим сферам, т. е. направлена по радиусам. Линии тока являются лучами, выходящими из начала координат.
, a Q = const или Q = Q (t). Ясно, что поверхностями равного потенциала j = const являются в этом случае поверхности r = const, т. е. концентрические сферы с центром в начале координат. Скорость v = grad j ортогональна к этим сферам, т. е. направлена по радиусам. Линии тока являются лучами, выходящими из начала координат.
Пусть Q > 0; тогда, так как grad j направлен в сторону роста j, то v направлена по r. Если Q < 0, то v направлена по - r (рис. 6). Величина скорости равна:
|(grad jr)| = 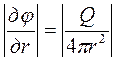 .
.
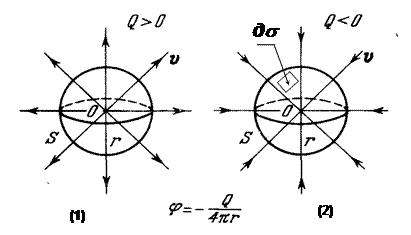 |
Рис. 6
Скорость стремится к нулю при r ® ¥ и к бесконечности при r ® 0. Точки нуль и бесконечность являются критическими. При Q > 0 (1) имеем
вытекание жидкости из начала координат во всех направлениях — это течение называется точечным пространственным источником.
Дата добавления: 2015-03-07; просмотров: 988;
