Денежные потоки и их оценка

Одним из основных элементов финансового анализа вообще и оценки инвестиционных проектов в частности является оценка де­нежного потока С₁, С₂, ... , С_п, генерируемого в течение ряда времен­ных периодов в результате реализации какого-либо проекта или функционирования того или иного вида активов. Элементы потока С_k, могут быть либо независимыми, либо связанными между собой определенным алгоритмом. Временные периоды чаще всего предпо­лагаются равными. Кроме того, для простоты изложения материала в этой главе предполагается, что элементы денежного потока явля­ются однонаправленными, т. е. нет чередования оттоков и притоков денежных средств. Также считается, что генерируемые в рамках од­ного временного периода поступления имеют место либо в его нача­ле, либо в его конце, т. е. они не распределены внутри периода, а сконцентрированы на одной из его границ. В первом случае поток называется потоком пренумерандо, или авансовым, во втором — по­током постнумерандо.

На практике большее распространение получил поток постнуме­рандо, в частности, именно этот поток лежит в основе методик ана­лиза инвестиционных проектов. Некоторые объяснения этому можно дать, исходя из общих принципов учета, согласно которым принято подводить итоги и оценивать финансовый результат того или иного действия по окончании очередного отчетного периода. Что касается поступления денежных средств в счет оплаты, то на практике оно чаще всего распределено во времени неравномерно и потому удобнее условно отнести все поступления к концу периода. Благодаря этому соглашению формируются равные временные периоды, что позволя­ет разработать удобные формализованные алгоритмы оценки. Поток пренумерандо имеет значение при анализе различных схем накопле­ния денежных средств для последующего их инвестирования.

Оценка денежного потока может выполняться в рамках решения двух задач: (а) прямой, т. е. проводится оценка с позиции будущего (реализуется схема наращения); (б) обратной, т. е. проводится оцен­ка с позиции настоящего (реализуется схема дисконтирования).

Прямая задача предполагает суммарную оценку наращенного де­нежного потока, т. е. в ее основе лежит будущая стоимость. В част­ности, если денежный поток представляет собой регулярные начис­ления процентов на вложенный капитал (Р) по схеме сложных про­центов, то в основе суммарной оценки наращенного денежного потока лежит формула (9.2).

Несложно показать, что будущая стоимость исходного денежного потока постнумерандо FV_pst может быть оценена как сумма наращен­ных поступлений, т. е. в общем виде формула имеет вид:

Обратная задача предполагает суммарную оценку дисконтирован­ного (приведенного) денежного потока. Поскольку отдельные эле­менты денежного потока генерируются в различные временные ин­тервалы, а деньги имеют временную ценность, непосредственное их суммирование невозможно. Приведение элементов денежного потока к одному моменту времени осуществляется с помощью формулы (9.3). Основным результатом расчета является определение общей величины приведенного денежного потока. Используемые при этом расчетные формулы различны в зависимости от вида потока — пост­нумерандо или пренумерандо. Именно обратная задача является ос­новной при оценке инвестиционных проектов.

В частности, приведенная стоимость денежного потока постнуме­рандо PV_pst в общем случае может быть рассчитана по формуле:

Несложно показать, что для потоков пренумерандо формулы (9.4) и (9.5) трансформируются следующим образом:

Одним из ключевых понятий в финансовых и коммерческих рас­четах является понятие аннуитета. Логика, заложенная в схему ан­нуитетных платежей, широко используется при оценке долговых и долевых ценных бумаг, в анализе инвестиционных проектов, а так­же в анализе аренды.

Аннуитет представляет собой частный случай денежного потока. Известны два подхода к его определению. Согласно первому подхо­ду аннуитет представляет собой однонаправленный денежный поток, элементы которого имеют место через равные временные интервалы. Второй подход накладывает дополнительное ограничение, а именно: элементы денежного потока одинаковы по величине. В дальнейшем изложении материала мы будем придерживаться именно второго подхода. Если число равных временных интервалов ограничено, ан­нуитет называется срочным. В этом случае:

Для оценки будущей и приведенной стоимости аннуитета можно пользоваться вышеприведенными формулами, вместе с тем благода­ря специфике аннуитетов в отношении равенства денежных поступ­лений они могут быть существенно упрощены.

В частности, для решения прямой задачи оценки срочных аннуи­тетов постнумерандо и пренумерандо при заданных величинах регу­лярного поступления (А) и процентной ставке (г) можно воспользо­ваться формулами (9.8) и (9.9):

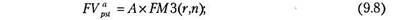
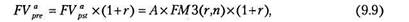
где

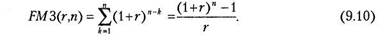
Экономический смысл FM3(r,n), называемого мультиплицирую­щим множителем для аннуитета, заключается в следующем: он пока­зывает, чему будет равна суммарная величина срочного аннуитета в одну денежную единицу (например один рубль) к концу срока его действия. Предполагается, что производится лишь начисление де­нежных сумм, а их изъятие может быть сделано по окончании срока действия аннуитета. Множитель FM3(r,n) часто используется в фи­нансовых вычислениях, и поскольку легко заметить, что его значе­ния в общем виде зависят лишь от r и п, они также табулированы.

Для решения обратной задачи оценки срочных аннуитетов постну­мерандо и пренумерандо, являющейся основной при анализе инвести­ционных проектов, денежные притоки которых имеют вид аннуитет­ных поступлений, можно воспользоваться формулами (9.11) и (9.12):

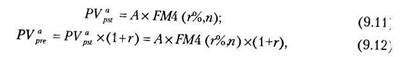
где

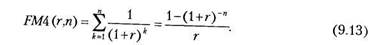
Экономический смысл FM4(r,n), называемого дисконтирующим множителем для аннуитета, заключается в следующем: он показыва­ет, чему равна с позиции текущего момента величина аннуитета с регулярными денежными поступлениями в размере одной денеж­ной единицы (например один рубль), продолжающегося п равных периодов с заданной процентной ставкой г. Значения этого множите­ля также табулированы.

При выполнении некоторых инвестиционных расчетов использу­ется техника оценки бессрочного аннуитета. Аннуитет называется бессрочным, если денежные поступления продолжаются достаточно длительное время (в западной практике к бессрочным относятся ан­нуитеты, рассчитанные на 50 и более лет).

В этом случае прямая задача смысла не имеет. Что касается об­ратной задачи, то ее решение для аннуитета постнумерандо делается на основе формулы:

Приведенная формула используется для оценки целесообразности приобретения бессрочного аннуитета. В этом случае известен размер годовых поступлений; в качестве коэффициента дисконтирования r обычно принимается гарантированная процентная ставка (например процент, предлагаемый государственным банком). Достаточно пол­ную и систематизированную сводку формул и методов прикладной финансовой математики, а также примеры их использования можно найти в (Ковалев, Уланов).