Поле бесконечной однородно заряженной плоскости
 Поверхностно распределенный заряд характеризуется поверхностной плотностью заряда
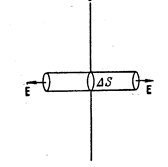
Поверхностно распределенный заряд характеризуется поверхностной плотностью заряда 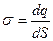 . Рассмотрим поле, создаваемое бесконечной плоскостью, заряженной с постоянной поверхностной плотностью s; для определенности будем считать заряд положительным. Из соображений симметрии вытекает, что напряженность в любой точке поля имеет направление, перпендикулярное к плоскости и в симметричных относительно плоскости точках напряженность поля будет одинакова по величине и противоположна по направлению. Представим себе мысленно цилиндрическую поверхность с образующими, перпендикулярными к плоскости, и основаниями величины DS, расположенными относительно плоскости симметрично. Применим к этой поверхности теорему Гаусса. В соответствии со сказанным в каждой точке основания Е одинаково и перпендикулярно основанию, поэтому суммарный поток через оба основания будет равен 2ЕDS. Поток вектора
. Рассмотрим поле, создаваемое бесконечной плоскостью, заряженной с постоянной поверхностной плотностью s; для определенности будем считать заряд положительным. Из соображений симметрии вытекает, что напряженность в любой точке поля имеет направление, перпендикулярное к плоскости и в симметричных относительно плоскости точках напряженность поля будет одинакова по величине и противоположна по направлению. Представим себе мысленно цилиндрическую поверхность с образующими, перпендикулярными к плоскости, и основаниями величины DS, расположенными относительно плоскости симметрично. Применим к этой поверхности теорему Гаусса. В соответствии со сказанным в каждой точке основания Е одинаково и перпендикулярно основанию, поэтому суммарный поток через оба основания будет равен 2ЕDS. Поток вектора 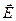 через боковую поверхность равен нулю, так как в каждой точке этой поверхности
через боковую поверхность равен нулю, так как в каждой точке этой поверхности 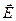 ^
^ 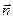 (cos a = 0).Следовательно, полный поток через рассматриваемую поверхность будет равен 2ЕDS. Внутри поверхности заключен заряд sDS. Согласно теореме Гаусса должно выполняться условие 2ЕDS=sDS/e0 откуда E=s/2e0
(cos a = 0).Следовательно, полный поток через рассматриваемую поверхность будет равен 2ЕDS. Внутри поверхности заключен заряд sDS. Согласно теореме Гаусса должно выполняться условие 2ЕDS=sDS/e0 откуда E=s/2e0
Полученный нами результат не зависит от длины цилиндра. Таким образом, на любых расстояниях от плоскости напряжённость поля одинакова по величине. Поэтому бесконечно равномерно заряженная плоскость создает в окружающем пространстве однородное поле.
Дата добавления: 2015-03-07; просмотров: 1075;
