Взаимное положение прямой и плоскости

Прямая относительно плоскости может занимать следующие положения: принадлежать плоскости, быть параллельной ей и пересекать ее (под прямым углом и произвольным углом). Первый случай был рассмотрен ранее (см. 1.4.3.). Рассмотрим случаи, когда прямая параллельна и перпендикулярна плоскости.

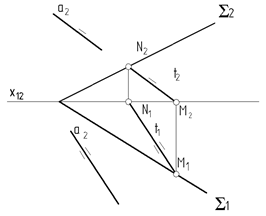1. Прямая а параллельна плоскости S, если она параллельна прямой t, принадлежащей этой плоскости: а ‖ t , t Î S Þ a ‖ S.

m1 m2 d1 l2 l1 d2 n1

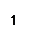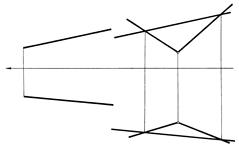
Рис. 59

На рис. 59 показаны прямые, параллельные плоскостям, заданным различными способами:

d ‖ Q ( m ∩ n), т.к. d ‖ ℓ , ℓ Î Q; d₂ ‖ ℓ₂ , d₁ ‖ ℓ₁.

а ‖ S, т.к. а ‖ t , t Î S Þ a ‖ S.

2. Прямая перпендикулярна плоскости S, если она перпендикулярна двумя пересекающимся прямым этой плоскости. В качестве пересекающихся прямых на плоскости выбирают горизонталь h и фронталь ¦. В этом случае можно воспользоваться свойствами проекций прямого угла:

a ^ h, a ^ ¦, h Ⴖ ¦, h Ì S, ¦ Ì S Þ а ^ S.

При этом прямые углы между прямой а и прямыми h и ¦ на соответствующие плоскости проекций спроецируются в натуральную величину: а₁ ^ h₁, а₂ ^ ¦₂.

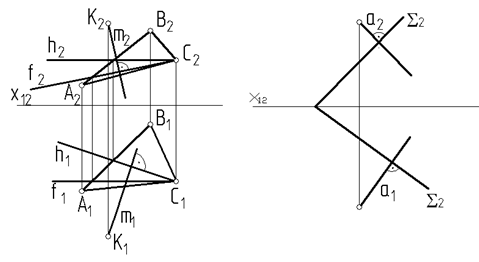
На рис. 60 показаны прямые, перпендикулярные плоскостям, заданным различными способами: m₁ ^ h₁, m₂ ^ ¦₂, h ∩ ¦, h Î ABC, ¦ Î ABC Þ m ^ ABC.

Если плоскость задана следами, то горизонталью и фронталью плоскости являются ее пересекающиеся следы (см. 1.4.4.).

а₁ ^ S₁, а₂ ^ S₂, S₁ Ⴖ S₂ Þ а ^ S.

Рис. 60