Прямая и точка в плоскости

Выбрать точку в некоторой плоскости произвольно, не связывая ее с другими элементами плоскости, невозможно.

Точка принадлежит плоскости, если она находится на прямой линии этой плоскости.

Прямая принадлежит плоскости, если она проходит:

1) через две точки, принадлежащие этой плоскости;

2) через точку, принадлежащую данной плоскости и параллельно любой прямой этой плос-

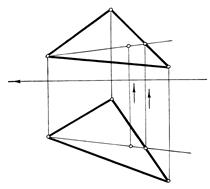Рис. 51

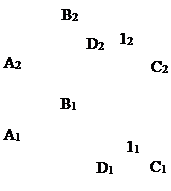кости.

X₁₂

Для построения точки, лежащей в плоскости, предварительно строят прямую, лежащую в данной плоскости, и на этой прямой затем строят точку. Например, требуется найти фронтальную (D₂) проекцию точки D, принадлежащей плоскости треугольника АВС, если задана ее горизонтальная проекция D₁ (рис. 51).

Сначала строим горизонтальную проекцию любой прямой, проходящей через D₁, допустим через А₁, до пересечения со стороной ВС (В₁С₁). Отмечаем точку 1_1.1₂ Î В₂С₂. Фронтальная проекция прямой А₁ проходит через фронтальные

проекции точек А и 1. D₂ Î А₂1₂.

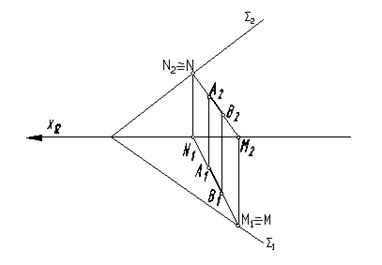Прямая принадлежит плоскости заданной следами, если ее следы принадлежат соответствующим следам плоскости. АВ Î S, т.к. N₂ Î S₂; М₁ Î S₁

Рис. 52

Справедливо и обратное условие, если следы прямой принадлежат следам плоскости, то эта прямая принадлежит плоскости. Используя это свойство, можно перейти от любого задания плоскости к заданию ее следами.

<13 14 151617 18 19 >

Дата добавления: 2015-02-25; просмотров: 825;