Взаимное положение плоскостей

Две плоскости относительно друг друга могут быть параллельны и перпендикулярны.

1. Если две пересекающиеся прямые а и b одной плоскости параллельны двум пересекающимся прямым c и d одной плоскости параллельны двум пересекающимся прямым с и d другой плоскости, то данные плоскости Q и S параллельны (рис. 61):

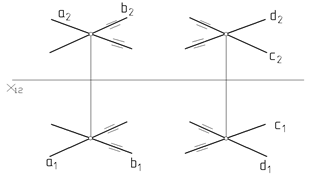
а ‖ с, b ‖ d, Q (а Ⴖ b), S ( с Ⴖ d) Þ Q ‖ S.

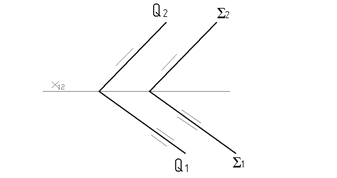
Рис. 61 Рис. 62

Плоскости, заданные следами, будут параллельны тогда, когда параллельны одноименные (соответствующие) следы этих плоскостей, т.к. следы плоскости мы рассматриваем, как две пересекающиеся прямые:

Q₁ ‖ S₁, Q₂ ‖ S₂ Þ Q ‖ S

2. Две плоскости взаимно перпендикулярны, если:

а) одна из них проходит через перпендикуляр к другой плоскости;

б) одна из плоскостей проводится перпендикулярно к прямой, лежащей в другой плоскости. Рассмотрим оба эти случая.

Через прямую АВ необходимо провести плоскость Q, перпендикулярную заданной плоскости S (CDE) (рис. 63).

Решение задачи сводится к построению перпендикуляра, проведенного из точки А или В на плоскость CDE. В плоскости CDE проведем горизонталь h и фронталь ¦. Из точки В проведем перпендикуляр к фронтали и горизонтали:

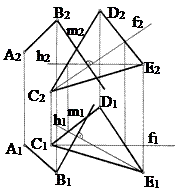
m₂ ^ ¦₂, m₁ ^ h₁ .

Так как прямая m Ì Q (AB Ⴖ m), a m ^ CDE Þ Q ^ CDE.

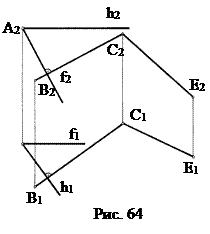
Через точку А необходимо провести плоскость перпендикулярную заданной плоскости P (BC ∩ CE) (рис. 64).

пересекающими прямыми должны

быть горизонталь h и фронталь ¦. Построим через точку А плоскость Q(h∩¦), при этом h₁^В₁С₁, ¦₂ ^ В₂С₂. Отметим, что плоскость Q ^ ВС по определению, ВС Ì Р (ВС ∩ СЕ) Þ Q ^ Р.