Пересечение прямой с плоскостью
|
|
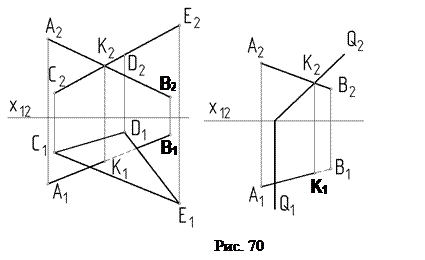 Рассмотрим примеры пересечения прямой АВ с плоскостью частного положения, в данном случае плоскость S (CDE) и Q, являются фронтальнопроецирующими.
Рассмотрим примеры пересечения прямой АВ с плоскостью частного положения, в данном случае плоскость S (CDE) и Q, являются фронтальнопроецирующими.
Плоскость, перпендикулярная к плоскости проекций, проецируется на нее в виде прямой линии. На этой прямой (проекции плоскости) находится и проекция точки пересечения некоторой прямой с заданной плоскостью.
На рис. 70 а, б фронтальная проекция точки пересечения прямой АВ с плоскостью S (CDE) и Q определяется: К2 = А2В2 Ⴖ С2D2E2, а К1 Î А1В1; К2 = А2В2 Ⴖ Q2, а К1 Î А1В1;
 Так как прямая АВ в направлении от К к В находится под плоскостью S и Q, то на чертеже часть горизонтальной проекции К1В1 проведена штриховой линией.
Так как прямая АВ в направлении от К к В находится под плоскостью S и Q, то на чертеже часть горизонтальной проекции К1В1 проведена штриховой линией.
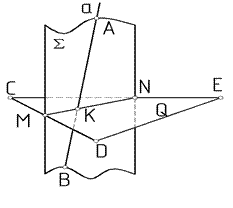
На рис. 71 показано построение точки К пересечения прямой а (АВ) с плоскостью Q (CDE). Для этого прямая а заключена в плоскость S и определена линия пересечения плоскостей S и Q: MN = Q Ⴖ S .
Прямые АВ и MN принадлежат одной плоскости S и пересекаются в точке К, а так как прямая MN принадлежит заданной плоскости Q (CDE), то точка К является точкой пересечения прямой а (АВ) с плоскостью Q (CDE).
Рис. 71 Задачу на пересечение прямой с плоскостью общего положения необходимо решать по следующей схеме (рис. 72):
1. Через данную прямую АВ необходимо провести вспомогательную плоскость частного положения (S - горизонтально проецирующая плоскость).
2. Построить линию пересечения МN ( М1N1, М2N2 ) данной плоскости CDE и вспомогательной S.
3.
|
4. Определить видимость взаимного пересечения. Для определения видимости взаимного пересечения прямой и плоскости воспользуемся методом конкурирующих точек.
Прямые АВ и CD скрещиваются. На плоскости проекций П2 эти прямые имеют совпадающие проекции точек 12≡22. По расположению горизонтальных проекций точек 11 и 21 заключаем, что точка 1 расположена ближе к наблюдателю, поэтому участок прямой 2К находится за плоскостью треугольника CDE и на фронтальной проекции будет невидим. Аналогично определяем видимость взаимного пересечения и на горизонтальной плоскости проекций. Прямые АВ и DЕ скрещиваются. На плоскости проекций П1 эти прямые имеют совпадающие проекции точек 31≡41 . По расположению фронтальных проекций точек 32 и 42 заключаем, что точка 4 расположена выше точки 3, поэтому участок прямой 3К находится под плоскостью треугольника CDE и на горизонтальной проекции будет невидим.
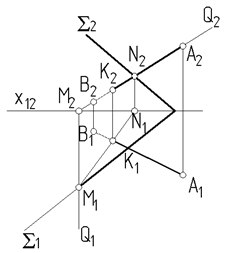 На рис. 73 показан пример определения точки К пересечения прямой АВ с плоскостью S , заданной следами.
На рис. 73 показан пример определения точки К пересечения прямой АВ с плоскостью S , заданной следами.
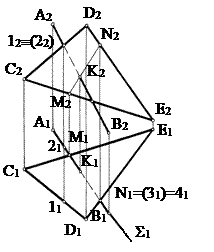 |
Рис. 72 Рис. 73
Прямую АВ заключаем во фронтально проецирующую плоскость Q:
Q Ì АВ, Q ^ П2 , Q1 ^ Х1 , Q2 ≡ А2В2 и определяем линию пересечения MN плоскостей S и Q (MN = S Ⴖ Q ). Линия пересечения плоскостей проходит через точки пересечения одноименных следов этих плоскостей (M = S1 Ⴖ Q1, N = S2 Ⴖ Q2 ). Точка пересечения прямых АВ и MN и есть искомая точка пересечения прямой АВ с плоскостью S. Видимость пересечения определена методом конкурирующих точек.
Контрольные задания по теме “Плоскость”
1. Через точку К, принадлежащую плоскости Р, провести линию наибольшего наклона к плоскости проекций П2. Определить Н.В этой линии.
| |||||||||||||||||||||||
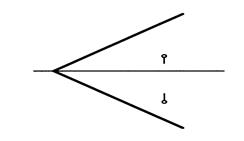
2. Через прямую АВ провести фронтально проецирующую плоскость под углом 300 к плоскости П1.
| |||||||||||||||||||||||
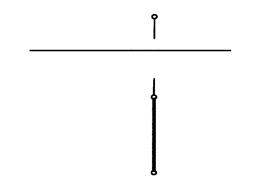
3. Записать название плоскости треугольника АВС. Определить удаление от плоскости проекций П1 точки пересечения прямой MN с плоскостью треугольника АВС.
| |||||||||||||||||||||||
|
4. Найти точку пересечения прямой MN c плоскостью S (т.К). Определить и записать ее удаление от плоскости П1. Какие из отрезков будут видимы: К2N2 или К2M2, и К1N1 или К1М1?

| |||||||||||||||||||||||
5. Построить линию пересечения плоскостей и определить угол наклона этой линии к плоскости П1.
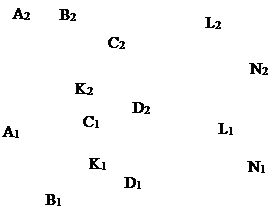 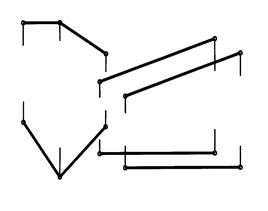
| |||||||||||||||||||||||
6. Построить горизонтальную проекцию M1N1 отрезка MN при условии его параллельности плоскости треугольника АВС. Определить угол наклона отрезка MN к плоскости проекций П2.
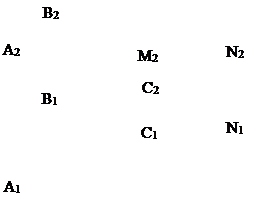 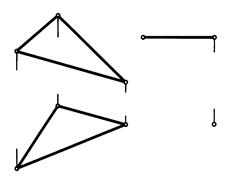
| |||||||||||||||||||||||
| 7.
  Определить расстояние от точки А до плоскости S. Определить расстояние от точки А до плоскости S.
| |||||||||||||||||||||||
8. Через прямую MN провести плоскость, перпендикулярную заданной, определить угол наклона построенной плоскости к плоскости проекций П1.
|
|
|
|
 Пример 1. Определить расстояние от точки S до плоскости S (АВС) (рис. 74).
Пример 1. Определить расстояние от точки S до плоскости S (АВС) (рис. 74).
 | |||||
 | |||||
|
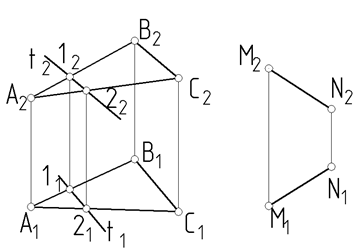
Рис. 74 Рис. 75
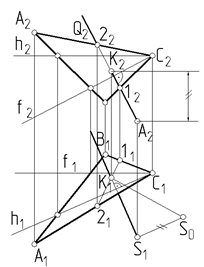
Строим перпендикуляр ℓ(ℓ1, ℓ2) из точки S (S1, S2) на плоскость S (АВС): ℓ1^ h1; ℓ2≡ ^ ¦2: далее находим точку К (К1К2) пересечения перпендикуляра ℓ с плоскостью S:
ℓ Ì Q, Q ^ П2 , Q2 ≡ ℓ2, К = ℓႶ 12, (К1 = ℓ1Ⴖ 1121; К2Îℓ2). Расстояние от точки S до плоскости S равно натуральной величине отрезка ÷ SК÷, т.е. S0 К1 .
Пример 2. Определить построением параллельность прямой MN и плоскости Q (АВС) (рис.75).
Прямая будет параллельна плоскости, если она параллельна хотя бы одной прямой, принадлежащей этой плоскости. Обязательно должно соблюдаться условие: прямые будут параллельны, если на чертеже их одноименные проекции параллельны.
Для этого строим на плоскости П2 (можно П1) прямую t2 ‖ M2 N2, t Î АВС. Так как t1 ∦ M1 N1 , можно сделать вывод, что прямая MN не параллельна заданной плоскости Q (АВС).
Дата добавления: 2015-02-25; просмотров: 2007;