Позиционные и метрические задачи

К позиционным задачам относятся задачи на определение общих элементов различные геометрических образов. Это задачи, где требуется установить взаимное положение и взаимную принадлежность рассматриваемых геометрических форм: найти точку на линии или плоскости (поверхности), найти точку пересечения прямой линии с плоскостью (поверхностью) или линию пересечения плоскостей (поверхностей) и т.д. Некоторые из этих задач рассматривались в предыдущих разделах. Среди различных позиционных задач можно выделить две основные задачи: пересечение прямой общего положения с плоскостью общего положения и пересечение плоскостей общего положения. При решении позиционных задач не рассматриваются метрические свойства элементов, т.е. те свойства, которые могут быть выявлены лишь в результате измерения. Параллельность геометрических образов является частным случаем их пересечения, т.к. параллельные прямые пересекаются в несобственной точке, а параллельные плоскости – по несобственной прямой.

Метрическими будем называть задачи, решение которых связано с определением, измерением линейных и угловых размеров геометрических образов.При ортогональном проецировании различные геометрические образы, произвольно расположенные в пространстве, проецируются на плоскости проекций с искажением, при этом искажаются их линейные и угловые характеристики. Определение неискаженных величин линейных и угловых характеристик геометрических образов, произвольно расположенных в пространстве, по их проекциям и есть решение ряда метрических задач.

Все метрические задачи можно разделить на три группы:

1. Определение расстояний между двумя точками, точкой и прямой, двум параллельным прямым, скрещивающимися прямыми, точкой и плоскостью, двумя параллельными плоскостями;

2. Определение углов между двумя прямыми, прямой и плоскостью, двумя плоскостями;

3. Определение величин плоских фигур, произвольно расположенных в пространстве.

Решение ряда метрических задач будет приведено во второй главе «Способы преобразования ортогонального чертежа».

Рассмотрим решение позиционных и метрических задач на примерах.

Позиционными называют задачи, где требуется установить взаимное положение и взаимную принадлежность рассматриваемых геометрических образов.

Метрическими называют задачи на определение длины линий, расстояний, размеров, углов, площадей и др.

Для решения метрических задач необходимо:

1) все задачи по определению расстояний привести к измерению расстояния между точками или к определению величины перпендикуляра, характеризующей искомое расстояние;

2) все задачи по определению углов привести к измерению угла между двумя пересекающимися линиями;

3) преобразовать заданные геометрические фигуры общего положения в такое положение, при котором искомые расстояния, углы и площади могут быть измерены непосредственно по чертежу.

Пример 1. Через прямую MN провести плоскость, перпендикулярную заданной плоскости АВС.

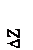
Определить угол наклона построенной плоскости к плоскости проекций П₁ (рис. 76).

План решения:

1. Через точку М проводим прямую l, перпендикулярную плоскости АВС. В треугольнике АВС АС является горизонталью, а АВ – фронталью плоскости. Поэтому проводим l₁ ^ A₁C₁; l₂ ^A₂ B₂.

2. Две пересекающиеся прямые MN и l задают плоскость, перпендикулярную заданной АВС. Перезададим построенную плоскость треугольником MNK.

3. Для определения угла наклона плоскости MNK к П₁ построим линию ската 12, которая перпендикуляр на горизонтали MN этой плоскости.

Рис.76 4. Определяем методом прямоугольного треуголь-

ника натуральную величину линии ската. Угол между натуральной величиной и ее горизонтальной проекцией будет искомым углом a.

Пример 2. Построить проекции высоты треугольника АВС, опущенной из вершины А на сторону ВС (рис. 77).

План решения.

1. Через точку А проводим плоскость Р (h ìü f), перпендикулярную прямой ВС. h₁ ^ B₁C₁; f₂ ^ B₂C₂.

2. Определяем точку пересечения прямой ВС с построенной плоскостью (т.О). Для этого через ВС проводим дополнительную проецирующую плоскость Q. Q ^ П₂. Строим линию пересечения построенной плоскости с заданной 12 = Q ìü АВС.

3. Отмечаем точку пересечения построенной линии с ВС. О = 12 ìü ВС.

4. Соединяем точки А и О, которые определяют высоту треугольника АВС.

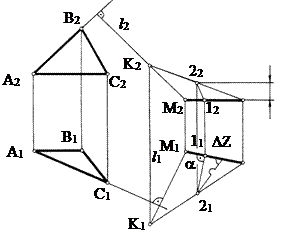
Пример 3. Через точку А провести прямую, пересекающую заданные прямые CD и EF

(рис. 78).

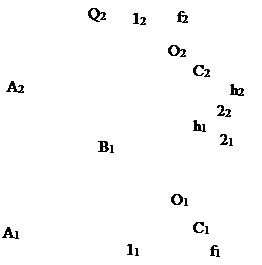
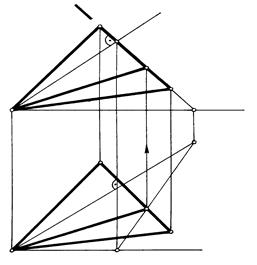
Рис.77 Рис. 78

План решения :

1. Через точку А и прямую EF проводим плоскость P (AF ìü EF).

2. Определяем точку пересечения прямой CD с плоскостью Р (т.О) (см. предыдущий пример 2).

3. Через точку А и полученную точку О проводим прямую АО. Она пересекает CD в точке О и пересекает EF, т.к. лежит с ней в одной плоскости, что и требовалось по условию задачи.

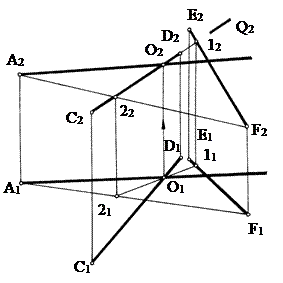
Пример 4. В плоскости Р провести прямую, перпендикулярную к прямой АВ и пересекающуюся с ней (рис. 79).

План решения:

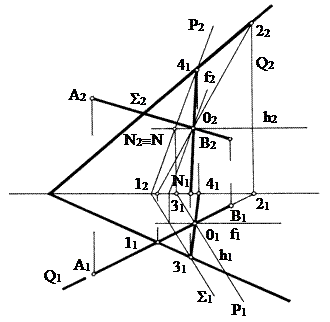1. Определяем точку О пересечения прямой АВ с плоскостью Р. Для этого через прямую АВ проводим горизонтально - проецирующую плоскость Q. Строим линию пересечения 12 плоскости P и Q. Отмечаем точку О пересечения линии 12 и АВ.

2. Через точку О проводим плоскость, перпендикулярную прямой АВ. Задаем ее горизонталью h и фронталью f, при этом h₁ ^ A₁B₁, f₂ ^ A₂B₂.

3. Перезадаем построенную плоскость h ìü f следами S₁, S₂, для этого определяем фронтальный след N горизонтали h и через него проводим S₂ || f₂, а через точку схода следов проводим S₁ || h₁.

4. Строим линию пересечения 34 плоскостей Р и S. Она будет искомой.