Вращение вокруг проецирующих прямых линий

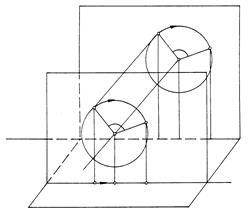
На рис. 85 изображены в системе П₂/П₁ некоторая точка А и ось вращения i,перпендикулярная к плоскости проекций П₂.

При вращении вокруг оси iточка А будет перемещаться по окружности, лежащей в плоскости Q, перпендикулярной к оси вращения i(параллельной плоскости П₂). Здесь плоскость Q – плоскость вращения; точка О – центр вращения (О = Q g i); отрезок АО – радиус вращения.

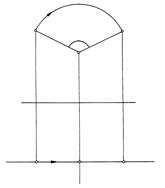
При повороте точки А на некоторый угол a фронтальная проекция будет перемещаться по дуге радиуса О₂А₂ (О₂А₂ = АО), а горизонтальная – по прямой А₁А₁', параллельной оси проекций Х₁₂. На рис. 86 эти же построения выполнены и на эпюре.

Пример1. Вращением вокруг прямой EF точку А ввести в плоскость BCD (рис. 87).

Точка А (А₁, А₂) вращается вокруг оси в горизонтальной плоскости Р(Р₂); центром вращения является точка О (О₁,О₂); радиусом вращения – отрезок АО (А₁О₁, А₂О₂). Плоскость Р(Р₂) пересекает заданную плоскость по горизонтали 12 (1₁2₁, 1₂2₂). Дугу окружности точки А пересекает горизонталь 12 данной плоскости в двух точках А'(А₁', А₂') и А"(А₁" А₂"). Эти точки являются искомыми.

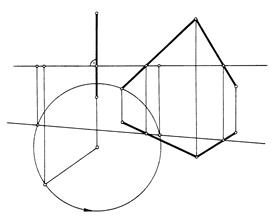
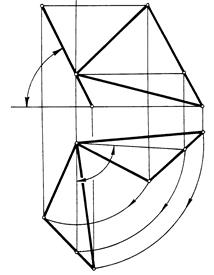
Рис. 87 Рис. 88

Вращение какой-либо фигуры вокруг проецирующих осей сводится к вращению точек этой фигуры.

Пример 2. Плоскость общего положения АВС преобразовать во фронтально-проецирующую плоскость (рис. 88).

Известно, что две плоскости взаимно перпендикулярны, если прямая линия одной плоскости перпендикулярна к другой плоскости. Выбираем в плоскости горизонталь и вращаем отсек плоскости вокруг горизонтально-проецирующей прямой i. Отсек плоскости перпендикулярен фронтальной плоскости проекций, если горизонталь данного отсека перпендикулярна к фронтальной плоскости проекций. Угол поворота плоскости АВС вокруг оси определяется углом между начальным и конечным положениями горизонтали этой плоскости (d) . Угол a – угол наклона фронтально-проецирующей плоскости АВ'С' к плоскости проекции П₁. На угол d поворачиваются горизонтальные проекции В₁' и С₁' вершин В и С данного треугольника. Фронтальные проекции В₂' и С₂' перемещаются по горизонтальным прямым линиям – следам плоскостей движения точек В и С.