Поле бесконечного заряженного цилиндра.

Рассмотрим поле, создаваемое бесконечной цилиндрической поверхностью радиуса R, заряженной с постоянной поверхностной плотностью s. Из соображений симметрии следует, что напряженность поля в любой точке должна быть направлена вдоль радиальной прямой, перпендикулярной к оси цилиндра, а величина напряженности может зависеть лишь от расстояния r от оси цилиндра. Представим себе замкнутую цилиндрическую поверхность радиуса r и высоты h , коаксиальную с заряженной поверхностью.

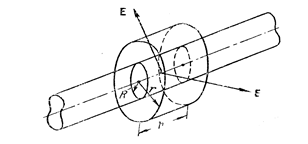Для боковой поверхности этого цилиндра

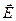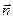çç , для оснований 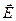^ 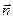(заряд считаем положительным). Следовательно, поток Е через эту замкнутую поверхность будет равен потоку через боковую поверхность цилиндра Е(r)× 2prh. Если r>R, внутрь Гауссовой поверхности попадает заряд q=lh, где l - линейная плотность заряда. Применяя теорему Гаусса, получаем.

Е(r)× 2prh= lh/e₀ откуда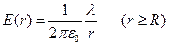

Если r<R, рассматриваемая замкнутая поверхность не содержит внутри зарядов, вследствие чего Е(r)=0, Таким образом, внутри заряженной цилиндрической поверхности бесконечной длины поле отсутствует.