Теорема Остроградского – Гаусса

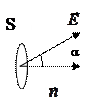Рассмотрим участок плоской поверхности площадью S, расположенный в однородном электрическом поле. Однородность означает постоянство вектора 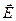во всех точках пространства. Ориентация поверхности задается положением вектора нормали 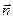к этой поверхности (см. рис.). Потоком вектора Ф_Е через рассматриваемую поверхность называется физическая величина, рассчитываемая по формуле

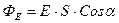. (4)

Если поле неоднородное, то рассматриваемую поверхность разбиваем на элементарные такие, что в пределах каждой вектор напряженности практически не меняется. Поток через каждую элементарную поверхность, в соответствие с формулой (4), будет равен

.

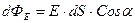Поток через всю поверхность будет равен интегралу от 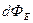по всей рассматриваемой поверхности .

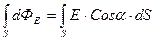Для потока вектора напряженности электростатического поля через замкнутую поверхность справедлива следующая теорема.

Теорема Остроградского – Гаусса: Поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на e₀.

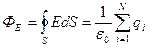. (5)

Наряду с вектором напряженности существует еще одна характеристика – вектор электрического смещения 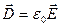( 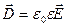) или вектор электрической индукции. Формула теоремы Остроградского – Гаусса для потока вектора электрической индукции имеет вид: .

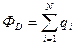Применение теоремы Остроградского – Гаусса к расчету полей