Поле заряженной сферической поверхности.

Поле, создаваемое сферической поверхностью радиуса R, за­ряженной с постоянной поверхностной плотностью s, будет, очевидно, отличаться центральной симметрией. Это означает, что направление вектора Е в любой точке проходит через центр сферы, а величина напряженно­сти является функцией расстояния r от центра сферы. Вообразим сферическую поверхность радиуса r. Для всех точек этой поверхности 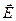^ 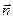. Если r > R. внутрь поверхности попадает весь заряд q, создающий рассматриваемое поле. Следовательно, 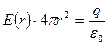откуда 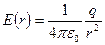(r³R)

Сферическая поверхность радиуса r, меньшего, чем R, не будет содержать зарядов, вследствие чего для r < R получается E (r) =0.

Таким образом, внутри сферической поверхности, заряженной с постоянной поверхностной плотностью s, ноле отсутствует. Вне этой поверхности поле имеет та­кой же вид, как поле точечного заряда той же величины, помещенного в центре сферы.