Работа сил электростатического поля

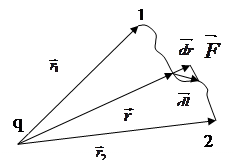
Рассмотрим поле, создаваемое неподвижным точечным зарядом q. В любой точке этого поля на пробный точечный положительный заряд q_П действует сила Кулона.

.

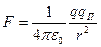При перемещение заряда q_П в поле заряда q эта сила совершает работу, которую, если вектор перемещения

равен 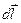, найдем по формуле : 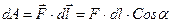. (6)

Так как 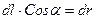- приращение модуля радиус-вектора 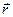при данном перемещении заряда q_П , то для работы, с учетом выражения (6), получим:

.

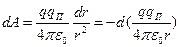То есть работа равна убыли некоторой функции координат 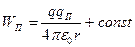, обусловленной взаимодействием зарядов, которую называют потенциальной энергией взаимодействия двух точечных зарядов, ее также можно назвать потенциальной энергией заряда q_П в поле заряда q или наоборот. Видим, что потенциальная энергия определена с точностью до произвольной постоянной, которую находят из граничных условий. В нашем случае положим Wп =0 на бесконечности, где взаимодействие отсутствует. Тогда const =0 и для потенциальной энергии взаимодействия двух точечных зарядов получим

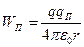. (7)

Чтобы найти работу сил поля по перемещению заряда q_П из точки 1 в точку 2 необходимо проинтегрировать dA вдоль траектории от начальной до конечной точек.

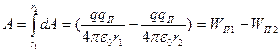. (8)

Так как W_П1 и W_П2 зависят только от значений радиус-вектора 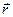в точках 1 и 2 соответственно, то из полученного выражения следует, что работа сил электростатического поля по перемещению заряда не зависит от траектории движения этого заряда, а определяется только его начальным и конечным положениями. Силы, обладающие такими свойствами, называются консервативными, а поля этих сил – потенциальными. В силу принципа суперпозиции полей полученное выражение (8) справедливо не только для поля точечного заряда, но и системы зарядов, то есть для любого электростатического поля. Следовательно, электростатическое поле – поле потенциальное. Независимость работы сил поля по перемещению заряда от траектории движения отражает потенциальный характер этого поля.

При движении заряда по замкнутой траектории работа сил электростатического поля равна нулю (А_замкн = 0), так как в этом случае W_П1=W_П2. Но формулу для работы можно представить в виде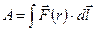

Так как 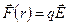то .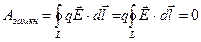

Данное равенство выполняется, если выполняется условие 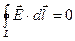. (9)

Интеграл, стоящий в этой формуле, носит название циркуляция вектора 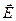по замкнутому контуру L. Таким образом, циркуляция вектора напряженности 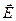электростатического поля по замкнутому контуру равна нулю. Это условие потенциального характера силового поля.

Из выражения (8) для потенциальной энергии заряда q_П в поле заряда q следует, что она пропорциональна величине пробного заряда. Отношение же ее к заряду q_П от его величины не зависит и может быть выбрана в качестве характеристики этой точки поля. Полученную величину называют потенциалом j поля в данной точке.

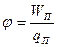. (10)

Потенциал – энергетическая характеристика электростатического поля. Так как потенциальная энергия определяется с точностью до произвольной постоянной, то это справедливо и для потенциала.

В соответствии с выражением (8) получается следующее выражение для потенциала поля заряда q на расстоянии r от него

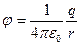. (11)

В формуле (10) q_П произвольный заряд, с помощью которого мы исследуем электростатическое поле. Опуская индекс П для потенциальной энергии заряда q в точке поля с потенциалом j , в соответствии с этой формулой, получим следующее выражение

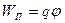. (12)

Тогда работа сил поля над зарядом 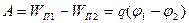. (13)

Если заряд удаляется из точки 1 в бесконечность то, так как j_¥ = 0, А_1¥ = qj.

Потенциал поля в данной точке численно равен работе, которую совершают силы электростатического поля над единичным положительным зарядом при удалении его из данной точки в бесконечность.

Итак, электрическое поле в данной точке можно описать с помощью векторной величины 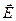и скалярной величины j. В курсе механики для поля консервативных сил было получено соотношение 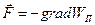, , 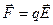а W_П = qj , тогда q 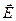= - grad(qj).

Откуда 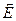= - grad j . (14)

Математически, градиентом какой либо функции, называется вектор, направленный в сторону наибыстрейшего увеличения данной функции по данному аргументу и равный скорости изменения функции по данному аргументу в этом направлении. Поэтому вектор напряженности поля в данной точке направлен в сторону наибыстрейшего уменьшения потенциала и показывает, на сколько изменяется потенциал поля на каждый метр удаления от заряда источника вдоль линии напряженности.

Помимо силовых линий для графического изображения полей используют эквипотенциальные поверхности. Эквипотенциальными называют поверхности все точки которых имеют одинаковый потенциал. Силовые линии перпендикулярны эквипотенциальным поверхностям.