Энергия заряженного конденсатора.
Пусть конденсатор имеет j1 – потенциал одной из обкладок с зарядом q+
и j2 – потенциал другой обкладки с зарядом q–
Используя формулу энергии системы зарядов (17) имеем
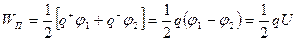 .
.
Исходя из определения электроемкости конденсатора полученную формулу сведем к виду
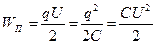 .
.
Подставим в эту формулу выражение для С, получим 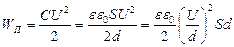 .
.
Так как напряженность поля в зазоре между обкладками конденсатора  , а Sd=V - объем пространства между обкладками, то
, а Sd=V - объем пространства между обкладками, то  .
.
Если поле однородно (поле плоского конденсатора), то энергия распределяется с постоянной плотностью 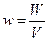 и
и 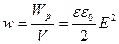 . С учетом
. С учетом 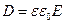 получим
получим
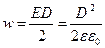 . (18)
. (18)
Зная плотность энергии поля в каждой точке пространства можно найти энергию поля, заключенную в любом объеме V. 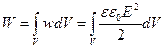
Дата добавления: 2015-03-07; просмотров: 898;
