Стрелочные улицы и съезды
Путь, на котором расположен ряд различных стрелочных переводов, называется стрелочной улицей.
Стрелочные улицы делятся на две основные категории:
-оконечные стрелочные улицы, т.е. расположенные в конце или в начале парка;
- срединные стрелочные улицы, пересекающие парк.
В свою очередь, указанные стрелочные улицы подразделяются на:
- прямолинейные, имеющие прямолинейные оси;
-ломанные стрелочные улицы, оси которых представляют ломанные линии;
-смешанные стрелочные улицы, представляющие сочетание первых двух.
Стрелочная улица обычно состоит из обыкновенных одиночных стрелочных переводов, расположенных на основном пути и ответвляющих от него боковых путей. Такие улицы находят широкое применение при устройстве приемо-отправочных парков с небольшим числом путей.
При выборе стрелочной улицы необходимо руководствоваться тем, чтобы рационально принятая стрелочная улица обеспечивала: безопасность движения поездов с установленной скоростью, наименьшие пробеги подвижного состава при маневрировании с ним, простоту в устройстве и содержании, возможность переустройства и развития станции, наименьшие расходы по устройству и содержанию.
Схема оконечной стрелочной улицы с ответвлениями в одну сторону от основного пути
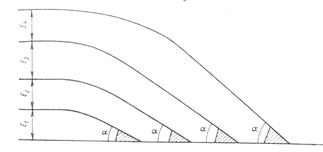
Схема оконечной стрелочной улицы, расположенной под углом α к основному пути
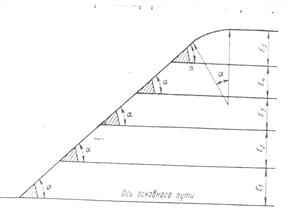
Схема промежуточной или срединной стрелочной улицы с перекрестными стрелочными переводами
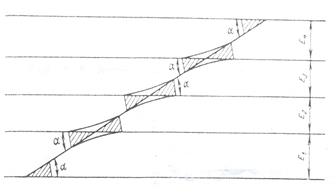
Съезды
Съезды представляют собой соединение двух близлежащих рельсовых путей посредством стрелочных переводов.
Съезды между двумя прямыми параллельными путями бывают:
- одиночные нормальные и сокращенные;
- перекрестные между двумя прямыми непараллельными путями;
- одиночные между двумя криволинейными путями.
Нормальный съезд между двумя прямыми параллельными путями представляет собой соединение путей посредством двух стрелочных переводов одной марки и одного типа.
Для определения размеров съезда, необходимых при его разбивке и укладке, должны быть известны:
Е – расстояние между осями путей;
N – число марки крестовины;
а - расстояние от переднего стыка рамных рельсов до центра стрелочного перевода Ц;
b – расстояние от центра стрелочного перевода до хвостового стыка крестовины, измеренное по оси пути перевода.
Схема разбивки нормального одиночного съезда

При этих данных необходимо: проверить возможность укладки такого съезда в зависимости от Е; определить расстояние Хнс между центрами стрелочных переводов и практическую длину Lнс нормального съезда.
Возможность укладки стрелочных переводов в нормальном съезде проверяют размером l0 – расстояние между хвостовыми концами крестовин двух переводов, измеренным по оси пути и съезда.
Наиболее целесообразна укладка в случае, когда l0 будет больше нуля. При этом если l0 равно нулю, то укладка возможна без каких-либо конструктивных изменений; если l0 больше нуля на незначительную величину, то, очевидно, следует рельсы, лежащие на нити бокового пути против крестовины, взять длиной, большей на величину l0; если l0 меньше нуля, то в большинстве случаев уложить стрелочные переводы в нормальный съезд не удается из-за невозможности укладки контррельсов по боковому пути.
Из прямоугольного треугольника ОСО видно, что сторона равная z, находится из выражения:
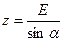 |  |
С другой стороны, z=b+l0+b или
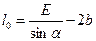 |
откуда
Расстояние Хнс также найдем из прямоугольного треугольника ОСО:
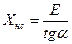
или имея в виду, что tga=1/N (марка крестовины),
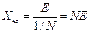 |
Практическая длина съезда
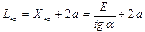 |
Дата добавления: 2015-03-03; просмотров: 9537;
