Стрелочные улицы под двойным углом крестовины, их расчет и условия применения (Савченко-31-32)

Стрелочные переводы 1, 2, 3 (рис. 23) располагаются по схеме попутной укладки. В общем случае расстояние между центрами переводов 1—2 и 2—3

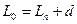
Зная 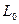можно определить расчетную ширину первого междупутья и ко­ординаты центра перевода 2: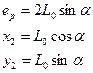

Расстояние 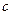между центрами переводов по улице, наклоненной под углом 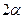, можно определить, соединив центры переводов 3 и 5 и опустив перпендикуляр из центра перевода 5 на путь 2. Линия 3—5 равна линии 2—4, т. е. равна 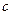. Из построенного вспомогательного треугольника с вершина­ми в точках 3 и 5 получим

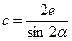
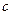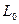Для определения координат центров двух переводов и вершин углов поворота используются найденные координаты центров перевода 2, а также известные расстояния и . Координаты вершины угла поворота крайнего пути определяются по формуле

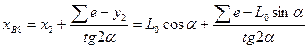
Для проверки вставки 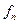на крайнем пути необходимо определить расстояние от центра перевода 2 до вершины угла поворота на крайнем пути, зная ординату :

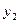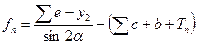
где 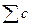— расстояние от центра перевода 2 до последнего перевода на прямом участке стрелочной улицы;

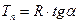— тангенс кривой на крайнем пути.

Вставки 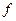определяются по формуле:

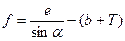
В том случае, когда первое междупутье должно быть одинаково с дру­гими, стрелочный перевод 3 для пути 2 укладывается на пути 1 на расстоянии 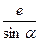от стрелочного перевода 1. При нечетном числе путей в парке схема стрелочной улицы изменяется, как показано пунктиром. Расстояние между переводом 1 (при его новом положении) и переводом 2 будет не 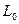, а несколь­ко больше

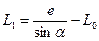
Принцип расчета других элементов сохраняется и для измененной схемы.

Достоинством стрелочной улицы под двойным углом крестовины является сокращение длины стрелочной зоны, а следовательно, и маневрово­го рейса. Применяется она преимущественно в горловинах приемо-отправочных парков, имеющих более четырех-пяти путей, и в головах небольших сортировочных парков (при отсутствии горки).

18) Принцип автоматизации расчетов соединений путей с применением ЭВМ (Савченко-37 + методичка)

Для расчетов сложных видов соединений путей целесообразно применение ЭВМ. Автоматизация этих расчетов обеспечивает высокую точность и резко сокращает затраты инженерно-технического труда. Особенно эффективно применение ЭВМ при проектировании переустройства горловин в стесненных условиях (когда необходимо отыскать оптимальное решение из большого числа возможных вариантов).

Разработка алгоритмов и программ для расчетов соединений путей на ЭВМ ведет­ся в нескольких проектных, учебных и научно-исследовательских институтах.

Более общее решение предложено канд. техн. наук К. К. Талем при разработке в ВНИИ трансп. стр-ва в 1966 г. алгоритма и программы расчета соединений путей на ЭВМ БЭСМ-2М. Чтобы охватить большее число случаев расчета с различными уравнениями, в программе выделена общая (постоянная) часть, предназначенная для решения любых уравнений, встречающихся при расчетах элементов соединений путей. Вторая часть программы, сменная для каждого вида расчета, является описанием структуры уравнений, решаемых в данном виде расчета. Для "стандартных" записей уравнений предложен метод их кодирования с заменой знаков действий и буквенных обозначений величин специальными кодами. «Стандартные» описания групп уравне­нии составлены не только для различных видов съездов и конечных соединений путей, но и для расчета некоторых стрелочных улиц (сокращенной, веерной, концентричес­кой), расчета расстояний между осями путей в кривых участках и др.

ПРИМЕНЕНИЕ ЭВМ ДЛЯ АВТОМАТИЗАЦИИ РАСЧЕТОВ И ПРОЕКТИРОВАНИЯ СОЕДИНЕНИЙ ПУТЕЙ

Отмечая определенную сложность и трудоемкость расчетов простых и сокращенных стрелочных улиц, можно сделать вы­вод о целесообразности использования ЭВМ особенно для сложных видов соединений путей.

Во ВНИИЖТе, МИИТе (МГУПС), ЛИИЖТе (ПГУПС) и других транспортных вузах рассматриваются теоретические вопросы и ведутся методические разработки по применению ЭВМ в проектировании железнодорожных стан­ций и узлов.

На кафедре "Станции и грузовая работа" РГУПС разработаны блок-схемы ипрограммы расчетов для следующих соединений путей и стре­лочных улиц:

1 - стрелочная улица под углом 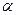к основному пути;

2 - стрелочная улица под углом 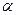на основном пути;

3 - веерная левосторонняя стрелочная улица;

4 - комбинированная стрелочная улица;

5 - стрелочная улица под углом 2 ;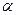

6 - сокращенная стрелочная улица;

7 - сокращенная стрелочная улица с путями под углом 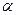от основного.

8 - сокращенная стрелочная улица с веерным отклонением путей;

9 - сокращенное соединение двух путей;

10 - сокращенный съезд;

11 - пучкообразная стрелочная улица на 4 пути.

Программы написаны на языке TURBO BASIC 1.0 для ЭВМ ШИЬ ЗС"Эверест" с использованием основных тригонометрических зависимо­стей, организации циклов и логических переходов для Расчета большо­го количества точек.