Системы счисления. Для удобства последующего преобразования дискретный сигнал подвергается кодированию(о кодировании см
Для удобства последующего преобразования дискретный сигнал подвергается кодированию(о кодировании см. в разделе Кодирование сигнала). Большинство кодов основано на системах счисления, причем использующих позиционный принцип образования числа, при котором значение каждой цифры зависит от ее положения в числе.
Примером позиционной формы записи чисел является та, которой мы пользуемся (так называемая арабская форма чисел). Так, в числах 123 и 321 значения цифры 3, например, определяются ее положением в числе: в первом случае она обозначает три единицы (т.е. просто три), а во втором – три сотни (т.е. триста).
Тогда полное число получается по формуле:
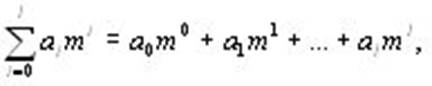
где l – количество разрядов числа, уменьшенное на 1,
i – порядок разряда,
m – основание системы счисления,
ai – множитель, принимающий любые целочисленные значения от 0 до m-1, и соответствующий цифре i-го порядка числа.
Например, для десятичного (m = 10) числа 345 его полное значение рассчитывается по формуле:
3*102 + 4*101 + 5*100 = 345.
Римские числа являются примером полупозиционной системы образования числа: так, в числах IX и XI знак I обозначает в обоих случаях единицу (признак непозиционной системы), но, будучи расположенным слева от знака X (обозначающего десять), вычитается из десяти, а при расположении справа – прибавляется к десяти. В первом случае полное значение числа равно 9, во втором – 11.
В современной информатике используются в основном три системы счисления (все – позиционные): двоичная, шестнадцатеричная и десятичная.
Двоичная система счисления используется для кодирования дискретного сигнала, потребителем которого является вычислительная техника. Такое положение дел сложилось исторически, поскольку двоичный сигнал проще представлять на аппаратном уровне. В этой системе счисления для представления числа применяются два знака – 0 и 1.
Шестнадцатеричная система счисления используется для кодирования дискретного сигнала, потребителем которого является хорошо подготовленный пользователь – специалист в области информатики. В такой форме представляется содержимое любого файла, затребованное через интегрированные оболочки операционной системы, например, средствами Norton Commander в случае MS DOS. Используемые знаки для представления числа – десятичные цифры от 0 до 9 и буквы латинского алфавита – A, B, C, D, E, F.
Десятичная система счисления используется для кодирования дискретного сигнала, потребителем которого является так называемый конечный пользователь – неспециалист в области информатики (очевидно, что и любой человек может выступать в роли такого потребителя). Используемые знаки для представления числа – цифры от 0 до 9.
Соответствие между первыми несколькими натуральными числами всех трех систем счисления представлено в таблице перевода:
| Десятичная система | Двоичная система | Шестнадцатеричная система |
| A | ||
| B | ||
| C | ||
| D | ||
| E | ||
| F | ||
Для различения систем счисления, в которых представлены числа, в обозначение двоичных и шестнадцатеричных чисел вводят дополнительные реквизиты:
· для двоичных чисел – нижний индекс справа от числа в виде цифры 2 или букв В либо b (binary – двоичный), либо знак B или b справа от числа. Например, 1010002 = 101000b = 101000B = 101000B = 101000b;
· для шестнадцатеричных чисел - нижний индекс справа от числа в виде числа 16 или букв H либо h (hexadecimal – шестнадцатеричный), либо знак H или h справа от числа. Например, 3AB16 = 3ABH = 3ABh = 3ABH = 3ABh.
Для перевода чисел из одной системы счисления в другую существуют определенные правила. Они различаются в зависимости от формата числа – целое или правильная дробь. Для вещественных чисел используется комбинация правил перевода для целого числа и правильной дроби.
Правила перевода целых чисел
Результатом перевода целого числа всегда является целое число.
Перевод из десятичной системы счисления в двоичную и шестнадцатеричную:
а) исходное целое число делится на основание системы счисления, в которую переводится (на 2 - при переводе в двоичную систему счисления или на 16 - при переводе в шестнадцатеричную); получается частное и остаток;
б) если полученное частное меньше основания системы счисления, в которую выполняется перевод, процесс деления прекращается, переходят к шагу в). Иначе над частным выполняют действия, описанные в шаге а);
в) все полученные остатки и последнее частное преобразуются в соответствии с таблицей перевода в цифры той системы счисления, в которую выполняется перевод;
г) формируется результирующее число: его старший разряд – полученное последнее частное, каждый последующий младший разряд образуется из полученных остатков от деления, начиная с последнего и кончая первым. Таким образом, младший разряд полученного числа – первый остаток от деления, а старший – последнее частное.
Пример 1. Выполнить перевод числа 19 в двоичную систему счисления:
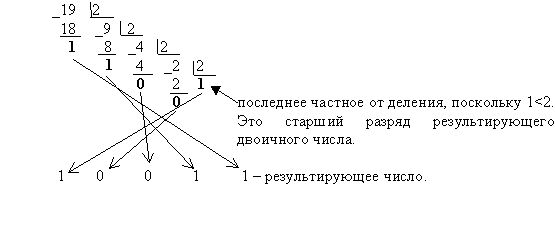
Таким образом, 19 = 100112.
Пример 2. Выполнить перевод числа 19 в шестнадцатеричную систему счисления:

Таким образом, 19 = 1316.
Пример 3. Выполнить перевод числа 123 в шестнадцатеричную систему счисления:

Здесь остаток 11 преобразован в шестнадцатеричную цифру В (см. таблицу) и после этого данная цифра вошла в число. Таким образом, 123 = 7В16.
Перевод из двоичной и шестнадцатеричной систем счисления в десятичную.
В этом случае рассчитывается полное значение числа по известной формуле.
Пример 4. Выполнить перевод числа 1316 в десятичную систему счисления. Имеем:
1316 = 1*161 + 3*160 = 16 + 3 = 19.
Таким образом, 1316 = 19.
Пример 5. Выполнить перевод числа 100112 в десятичную систему счисления. Имеем:
100112 = 1*24 + 0*23 + 0*22 + 1*21 + 1*20 = 16+0+0+2+1 = 19.
Таким образом, 100112 = 19.
Перевод из двоичной системы счисления в шестнадцатеричную:
а) исходное число разбивается на тетрады (т.е. 4 цифры), начиная с младших разрядов. Если количество цифр исходного двоичного числа не кратно 4, оно дополняется слева незначащими нулями до достижения кратности 4;
б) каждая тетрада заменятся соответствующей шестнадцатеричной цифрой в соответствии с таблицей.
Пример 6. Выполнить перевод числа 100112 в шестнадцатеричную систему счисления.
Поскольку в исходном двоичном числе количество цифр не кратно 4, дополняем его слева незначащими нулями до достижения кратности 4 числа цифр. Имеем:

В соответствии с таблицей 00112 = 112 = 316 и 00012 = 12 = 116.
Тогда 100112 = 1316.
Перевод из шестнадцатеричной системы счисления в двоичную:
а) каждая цифра исходного числа заменяется тетрадой двоичных цифр в соответствии с таблицей. Если в таблице двоичное число имеет менее 4 цифр, оно дополняется слева незначащими нулями до тетрады;
б) незначащие нули в результирующем числе отбрасываются.
Пример 7. Выполнить перевод числа 1316 в двоичную систему счисления.
По таблице имеем:
· 116 = 12 и после дополнения незначащими нулями двоичного числа 12 = 00012;
· 316 = 112 и после дополнения незначащими нулями двоичного числа 112 = 00112.
Тогда 1316 = 000100112. После удаления незначащих нулей имеем 1316 = 100112.
Дата добавления: 2015-03-03; просмотров: 940;
