Преобразования сигнала

Для преобразования непрерывного сигнала в дискретный используется процедура, которая называется квантованием. Различают два вида квантования – по времени и по уровню.

Квантование по времени– это замена непрерывной (по времени и по уровню) функции x(t)

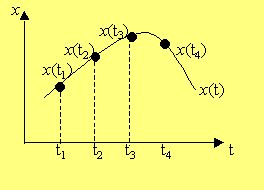
некоторым множеством непрерывных (по уровню) функций x(t_i) ( i = {1,2,3,4}):

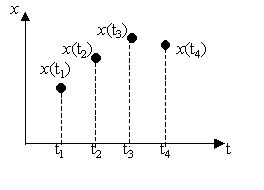
Очевидно, квантование по времени связано с потерей информации. В самом деле, дискретный сигнал не показывает, как ведет себя исходный сигнал в моменты времени, например, между t₃ и t₄. Иначе говоря, этот процесс связан с некоторой погрешностью ε, которая зависит от шага дискретизации Δt = t_i – t_i-1: при малых значениях шага дискретизации число точек замера высоко, и теряется мало информации; очевидно, картина обратная при больших шагах дискретизации. Погрешность квантования по времени ε в каждый момент времени t определяется по формуле:

ε(t) = x(t) – v(t),

где v(t) – функция восстановления, которая по дискретным значениям {x(t_i)}восстанавливает x(t).

Виды квантования по времениразличаются по регулярности отсчетов:

· равномерный вид, когда Δt постоянно;

· неравномерный вид, когда Δt переменно, причем этот вид, в свою очередь, делится на подвиды:

· адаптивный, когда Δt меняется автоматически в зависимости от текущего изменения сигнала. Это позволяет увеличивать шаг дискретизации, когда изменения сигнала x(t) незначительны, и уменьшать – в противном случае;

· программируемый, когда Δt изменяется оператором или в соответствии с заранее выставленными условиями, например, в фиксированные моменты времени.

Квантование по уровню - это преобразование непрерывных (по уровню) сигналов x(t_i), полученных в результате квантования по времени, в моменты отсчета t_i в дискретные. В результате непрерывное множество значений сигнала x(t_i) в диапазоне от x_min до x_max преобразуется в дискретное множество значений x_k – уровней квантования:

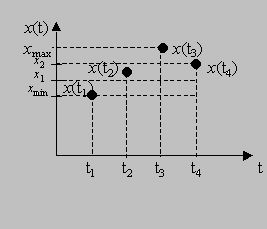
Шаг квантования Δx определяется по формуле:

Δx = x_j – x_j-1 .

Можно сказать, что квантование по уровню – это измерение сигнала. В самом деле, по последнему рисунку видно, что сигнал x(t₁) составляет 0 уровней квантования (k = 0), а сигнал x(t₄) – 2 уровня квантования (k = 2).

При квантовании по уровнюне всегда сигнал x(t_i) совпадает с уровнем квантования (см. сигнал x(t₂) на рисунке). В таком случае поступают одним из следующих способов:

1. x(t_i) отождествляют с ближайшим значением (в нашем примере – с x₂);

2. x(t_i) отождествляют с ближайшим меньшим (или большим) значением. Тогда при отождествлении с ближайшим большим значением сигнал x(t₂) отождествится с x₂ независимо от того, насколько близко он к этому уровню квантования находится. При отождествлении с ближайшим меньшим значением сигнал x(t₂) отождествится с x₁ также независимо от того, насколько близко он к этому уровню квантования находится.

Очевидно, и при квантовании по уровню возникает погрешность квантования ε(x_k):

ε(x_k) = x(t_i) - x_k.

Погрешность квантования по уровню тем меньше, чем меньше шаг квантования.

Виды квантования по уровню:

1. равномерное, когда диапазон изменения сигнала разбивается на m одинаковых частей. Тогда, зная размер шага квантования, для представления x_k достаточно знать число k.

2. неравномерное, когда диапазон изменения сигнала разбивается на m различных частей.