Перевод из двоичной и шестнадцатеричной систем счисления в десятичную.

В этом случае рассчитывается полное значение числа по формуле, причем коэффициенты a_i принимают десятичное значение в соответствии с таблицей.

Пример 3. Выполнить перевод из двоичной системы счисления в десятичную числа 0,1101₂.

Имеем:

0,1101₂ = 1*2^-1 + 1*2^-2 + 0*2^-3 +1*2^-4 = 0,5 + 0,25 + 0 + 0,0625 = 0,8125.

Расхождение полученного результата с исходным числом (см. пример 1) вызвано тем, что процедура перевода в двоичную дробь была прервана.

Таким образом, 0,1101₂ = 0,8125.

Пример 4. Выполнить перевод из шестнадцатеричной системы счисления в десятичную числа 0,D8D₁₆.

Имеем:

0,D8D₁₆ = 13*16^-1 + 8*16^-2 + 13*16^-3 = 13*0,0625 + 8*0,003906 + 13* 0,000244 = 0,84692.

Расхождение полученного результата с исходным числом (см. пример 2) вызвано тем, что процедура перевода в шестнадцатеричную дробь была прервана.

Таким образом, 0,D8D₁₆ = 0,84692.

Перевод из двоичной системы счисления в шестнадцатеричную:

а) исходная дробь делится на тетрады, начиная с позиции десятичной точки вправо. Если количество цифр дробной части исходного двоичного числа не кратно 4, оно дополняется справа незначащими нулями до достижения кратности 4;

б) каждая тетрада заменяется шестнадцатеричной цифрой в соответствии с таблицей.

Пример 5. Выполнить перевод из двоичной системы счисления в шестнадцатеричную числа 0,1101₂.

Имеем:

В соответствии с таблицей 1101₂ = D₁₆. Тогда 0,1101₂ = 0,D₁₆.

Пример 6. Выполнить перевод из двоичной системы счисления в шестнадцатеричную числа 0,0010101₂.

Поскольку количество цифр дробной части не кратно 4, добавим справа незначащий ноль:

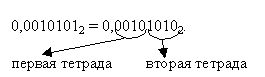
В соответствии с таблицей 0010₂ = 10₂ = 2₁₆ и 1010₂ = A₁₆.

Тогда 0,0010101₂ = 0,2A₁₆.

Перевод из шестнадцатеричной системы счисления в двоичную:

а) каждая цифра исходной дроби заменяется тетрадой двоичных цифр в соответствии с таблицей;

б) незначащие нули отбрасываются.

Пример 7. Выполнить перевод из шестнадцатеричной системы счисления в двоичную числа 0,2А_16.

По таблице имеем 2₁₆ = 0010₂ и А₁₆ = 1010₂.

Тогда 0,2А₁₆ = 0,00101010₂.

Отбросим в результате незначащий ноль и получим окончательный ответ: 0,2А₁₆ = 0,0010101₂

Правило перевода дробных чисел (неправильных дробей)

Напомним, что неправильная дробь имеет ненулевую дробную часть, т.е. у нее числитель больше знаменателя.

Результат перевода неправильной дроби всегда неправильная дробь.

При переводе отдельно переводится целая часть числа, отдельно – дробная. Результаты складываются.

Пример 1. Выполнить перевод из десятичной системы счисления в шестнадцатеричную числа 19,847. Перевод выполнять до трех значащих цифр после запятой.

Представим исходное число как сумму целого числа и правильной дроби:

19,847 = 19 + 0,847.

Как следует из примера 2 раздела Перевод целых чисел 19 = 13₁₆, а в соответствии с примером 2 раздела Перевод правильных дробей 0,847 = 0,D8D₁₆.

Тогда имеем:

19 + 0,847 = 13₁₆ + 0,D8D₁₆ = 13,D8D₁₆.

Таким образом, 19,847 = 13,D8D₁₆.