Спіральні структури (ревербератори) в міокарді.
Вперше спіральні структури в міокарді були відкриті у 1946 році мексиканським кардіохірургом А. Розенблютом та математиком Н. Вінером, який по праву вважається "батьком" кібернетики. У той рік А. Розенблют запросив свого друга Н. Вінера відпочити з ним, тоді ж він і розповів Н. Вінеру про небезпечну серцеву хворобу - фібриляцію, яка дуже часто призводить до миттєвої зупинки серця. І вони разом створили модель, яка показала, що при порушенні механічної однорідності серцевого м'язу - міокарду (така неоднорідність спостерігається біля витоку вени з серця) з'являється спіральна хвиля електричного збудження міокардіальних клітин. Ця спіральна хвиля отримала назву "ревербератор" (рис. 5.3). В подальшому вдалося довести, що ревербератори виникають не лише там, де порушується механічна неоднорідність, але і в точках, де з'являється неоднорідність по деякому прихованому параметру активного середовища, яким є міокард, - періоду рефрактерності (див. нижче). Саме ці точки стають джерелами появи спіральних хвиль (ревербераторів).

Рис. 5.3. Спіральна хвиля в серцевому м'язі кролика (з роботи М. Алессі, Ф. Бонке, Ф. Шопмана; цифрами позначені моменти часу в мілісекундах).
Прямим наслідком розмноження ревербераторів у міокарді є тахікардія (зміна нормального ритму роботи серця, а саме - збільшення частоти серцевих скорочень), а потім і фібриляція (хаотична пульсація серця). Розуміючи механізми появи ревербераторів, можна вести свідомий пошук ліків та інших немедикаментозних методів запобігання фібриляції. Треба підкреслити, що хімічний реактор, де відбувається періодична реакція Бєлоусова-Жаботинського, є тим активним аналоговим середовищем, в якому були зроблені успішні експерименти в цьому напрямі.
Сучасні підходи до основних синергетичних проблем самоорганізації та впорядкування використовують потужні та добре апробовані методи, на які спираються а) теорія фазових перетворень; б) теорія нелінійних коливань і автохвиль; в) кінетичні моделі типу "брюсселятора" і "орегонатора"; г) теорія катастроф та деякі інші підходи. Нижче ми зупинимося детальніше на цих питаннях.
Розпочнемо з аналізу сучасного стану і досягнень теорії фазових переходів, яка складає (поряд з іншими методами) наукову і методичну основу синергетики. В критичних точках, які визначають процеси самоорганізації і впорядкування, слід приділяти особливу увагу флуктуаційним ефектам. В останні 2-3 десятиліття досягнуто великих успіхів у з'ясуванні ролі флуктуацій - відхилень різних термодинамічних параметрів (густини, концентрації, температури, тиску тощо) від своїх середніх значень. Це стало можливим завдяки розвитку універсальних методів фізики фазових переходів і критичних явищ, заснованих на ідеях теорій масштабної інваріантності (скейлінгу) і ренор-малізаційної групи, які були розвинуті в роботах 0.3. Паташинського, В.Л. Покровського, М. Фішера, Л. Каданова, К. Вільсона та інших вчених.
Вихідним при побудові статистичної теорії фазових переходів є поняття параметра порядку та поля, спряженого йому в термодинамічному сенсі (табл. 5.2). Іншою принципово важливою характеристикою систем, в яких відбуваються фазові переходи, є радіус кореляції, який визначає ту відстань, на якій флуктуації параметра порядку, тобто їх відхилення від середніх значень, впливають одна на одну (корелюють між собою). З наближенням до точки фазового переходу величина радіуса кореляції сильно зростає. Таким чином, різним системам поблизу їх фазових переходів стає притаманною колективна взаємодія флуктуацій на великих відстанях та на значних часових інтервалах. Більш того, в поведінці цих систем з'являється універсальність, тобто їх властивості (рівняння стану, різні рівноважні та кінетичні характеристики) описуються однаковими законами, які називають масштабно-інваріантними або скейлінговими. Цей результат є дуже сильним і принциповим через те, що дослідивши детально критичну поведінку однієї системи (наприклад, рідини поблизу її критичної точки), можна перенести отримані результати на систему іншої природи (наприклад, магнетик, надпровідник, хімічно реагуючу систему тощо) за допомогою своєрідного "словника" (частина цього словника міститься у табл. 5.2), який пов'язує між собою відповідні величини систем різної природи.
Таблиця 5.2. Параметри порядку та спряжені поля для різних систем
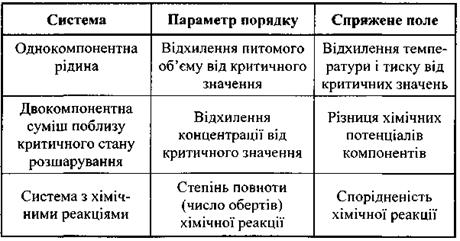
Залежність рівноважних та кінетичних властивостей від температури, зовнішнього поля та інших змінних поблизу точок фазових переходів характеризується степеневими законами, де показники степенів мають назву критичних індексів. Величини критичних індексів залежать від просторової розмірності системи, розмірності (числа компонентів) параметра порядку, а також від радіуса потенціалу взаємодії. Системи, що мають однакові значення цих характеристик (наприклад, є тривимірними, із скалярним параметром порядку і короткосяжним радіусом міжмолекулярної взаємодії), потрапляють в один і той самий "клас універсальності". Це означає, що такі системи, як однокомпонентна рідина чи бінарна рідка суміш, магнетик в так званому наближенні Ізінга, хімічно реагуюча система, система "медіатор-рецептор" у синаптичній щілині тощо, описуються поблизу своїх критичних точок однаковими степеневими скейлінговими законами.
Потрібно розрізняти рівноважні та нерівноважні фазові переходи. Для рівноважних фазових переходів, про які йшлося вище, притаманна поступова зміна таких параметрів, як тиск, температура, хімічні потенціали компонентів розчину тощо (ці параметри називають інколи "польовими"), а також стрибкоподібна зміна таких параметрів, як об'єм, ентропія, концентрації компонентів розчину тощо (ці параметри називають інколи "густинними"). У разі нерівноважних фазових переходів відбуваються різкі зміни в поведінці параметрів системи, які спричиняють появу впорядкованих структур. Ці процеси впорядкування і самоорганізації певною мірою нагадують рівноважні фазові переходи, де відбувається стрибкоподібна зміна "густин-них" параметрів. Проте суттєвою особливістю нерівноважних фазових переходів (на відміну від рівноважних) є те, що вони відбуваються у відкритих системах, в яких через взаємодію з навколишнім середовищем спостерігається від'ємна зміна (тобто зменшення) ентропії. Звичайно, нерівноважні фазові переходи (їх називають ще кінетичними фазовими переходами) є набагато різноманітнішими, ніж рівноважні (термодинамічні) фазові переходи.
Розглянемо загальні властивості відкритих систем, в яких існують різноманітні процеси впорядкування. На відміну від рівноважних утворень, які можуть бути описані та досліджені відомими методами термодинаміки та статистичної фізики, в нерівноважних системах реалізуються так звані дисипативні структури (цей термін вперше був введений І.Р. Пригожиним). Прикладом звичайних рівноважних структур є рідина чи кристал, які існують в залежності від температури, тиску та інших зовнішніх параметрів. Дисипативні структури утворюються завдяки потокам енергії, імпульсу, маси через границі системи. Типовим прикладом дисипативної структури є так звані комірки Бенара, які виникають в реальній в'язкій рідині при наявності в ній різниці температури. Коли рідина підігрівається знизу (існує потік тепла через нижню границю в такій відкритій системі), то раптово при деякому співвідношенні між товщиною шару рідини, різницею (градієнтом) температури, в'язкістю та іншими параметрами в раніше однорідній рідині виникають шестигранні утворення - комірки Бенара (рис. 5.4).

Рис. 5.4. Гексагональні комірки Бенара.
Такий процес є проявом взаємодії флуктуацій (відхилень параметрів системи від середніх значень). Роль взаємодії флуктуацій зростає і стає вирішальною поблизу критичних (біфуркаційних) точок. Ця взаємодія може стати настільки сильною, що існуюча раніше структура (в нашому випадку - однорідна рідина) руйнується. В ній з'являються більш впорядковані структури, які й називаються дисипативними.

Рис. 5.5. Гексагональні структури, що виникли на поверхні солоного озера Юмі в Болівії (фото К. Хірояма з "Дейлі Юміурі").
Дуже схожий до комірок Бенара вигляд мають гексагональні структури, що спостерігаються на висушеній поверхні солоного озера Юмі в Болівії (рис. 5.5). Можливо, це також є проявом синергетичних процесів, що виникають при конвекційній нестійкості нерівноважної відкритої системи. Значна схожість цих гексагональних структур дивує і є безумовним викликом людському розуму, як і поширеність спіральних структур у зовсім різних за своєю природою системах.
Інший тип впорядкування відкритої системи - це автохвипі та автокод иваїшя, що були розглянуті вище на прикладі хімічної реакції Бєлоусова-Жаботинського чи ревербераторів у міокарді. Відомими прикладами автохвиль і автоколивань є також хвиля поширення потенціалу дії (зміни електричного потенціалу) вздовж нервового волокна (аксона), хвиля горіння, автоколивання при гліколізі та фотосинтезі тощо.
Загальні риси всіх цих процесів полягають у наявності наступних спільних особливостей середовищ, де вони відбуваються:
1. Середовища, в яких поширюються автохвилі або автоколивання, є активними. У звичайних пасивних середовищах, де спостерігаються пружні, теплові або електромагнітні хвилі, енергія хвилі передається від джерела у віддалені точки з послабленням. На відміну від пасивних середовищ, в активних йдуть процеси накопичення енергії та її вивільнення при відповідному механізмі збудження.
2. Активні середовища мають три різні стани свого функціонування:
- стан спокою, який реалізується у відсутності зовнішніх впливів;
- стан збудження, який виникає при наявності зовнішніх впливів;
- стан рефрактерності, який виникає після зникнення збудження і протягом якого система повертається в стан спокою (якщо система перебуває у стані рефрактерності, вона не може бути переведена у стан збудження доти, доки вона не перейде у стан спокою).
3. Цікава властивість автохвильових процесів, в тому числі й ревербераторів в серцевому м'язі, пов'язана з так званим ефектом синхронізації. Суть цього ефекту полягає в тому, що коли в активному середовищі діють кілька джерел коливань і хвиль з різними частотами, то найстійкішими є коливання і хвилі з максимальною частотою. Іншими словами, всі коливання з меншими частотами подавляються коливаннями з більшими частотами.
4. Властивості автохвиль в активних середовищах і хвиль у пасивних середовищах досить сильно відрізняться (табл. 5.3). У цій таблиці, в останньому стовпчику, містяться відомості і про ще один тип впорядкованих структур - солітони (поодинокі хвилі).
Таблиця 5.3. Порівняння властивостей автохвиль в активних середовищах, хвиль у пасивних середовищах і солітонів
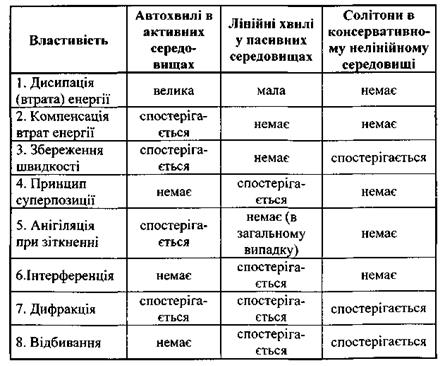
Вперше солітон був відкритий С. Расселом у 1834 році досить випадково, як часто й робляться великі відкриття. С. Рассел вивчав в той час рух барж різних форм, що мали різні швидкості, з метою надати рекомендації щодо будівництва барж у зв'язку з переходом від кінської тяги до парової. Саме проводячи ці спостереження, він відкрив солітон, про що так написав у своєму звіті "Доповідь про хвилі": "Я слідкував за рухом баржі, яку швидко тягнула вздовж вузького каналу пара коней, коли баржа раптово зупинилася; але маса води, яку баржа привела в рух, не зупинилася. Замість цього вона зібралася біля носа судна в стані божевільного руху, потім раптово залишила його позаду і покотилася вперед з дуже великою швидкістю, прийнявши форму великого одинокого підвищення, тобто водяного пагорба, який продовжував свій шлях вздовж каналу, не змінюючи своєї форми та не знижуючи швидкості". Нині солітони відкриті у багатьох середовищах - в магнетиках, надпровідниках, живих системах, атмосферах Землі та планет. Досить ймовірно, що солітони мали важливе значення для процесу еволюції Всесвіту. Хромодинаміка, сучасна теорія елементарних частинок, передбачає появу (поки що не відкритих експериментально) солітонів, які можуть нести магнітний заряд. Таким чином, справедливим є твердження, що наука про солітони інтенсивно розвивається в останні роки.
Зрозуміло, що методи синергетики повинні добре працювати у випадках, коли йдеться саме про кооперативну поведінку систем різної природи з утворенням впорядкованих структур. Нижче ми розглянемо приклади застосування синергетичних методів до деяких соціальних і політичних процесів.
Насамперед постає питання: чи можливо взагалі сподіватися на успіх при застосуванні подібних методів до об'єктів, які складаються з великої сукупності індивідуумів? Справді, поведінка окремого індивіда в складних ситуаціях, як правило, непередбачена, вона визначається дуже великою кількістю часто випадкових факторів. Тому зрозуміло, що скоріш за все неможливо створити детерміновану математичну модель такої поведінки окремої людини. Разом з тим, очевидно, можна сподіватися на досить точне передбачення середньостатистичної поведінки окремого представника даної соціальної групи. Саме в цьому випадку, тобто на рівні статистичних закономірностей, стають корисними математичні методи, що спираються на досягнення сучасної синергетики.
Спочатку зупинимося на застосуванні методів синергетики до соціології, зокрема на процесі формування громадської думки. Розглянемо приклад, який пов'язаний з цим процесом і відомий як експеримент С. Еша. Нехай людині показують кілька предметів різної довжини (рис. 5.6).
Питання, на яке треба дати відповідь, таке: "Як співвідносяться між собою довжини першого і останнього відрізків?" Як виявляється і це цілком зрозуміло, відповідь залежить від того, чи відомі людині результати попереднього опитування.
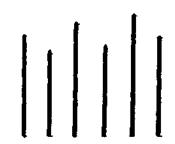
Рис. 5.6. Експеримент С. Еша (з книги Г. Хакена "Синергетика. Иерархия неустойчивостей в са-моорганизующихся системах и устройствах").
Так, наприклад, якщо в результаті попереднього опитування 60% опитуваних відповіли, що останній відрізок довший за перший, то людина З більшою ймовірністю підтвердить цей висновок. Насправді, обидва відрізки мають однакові довжини.
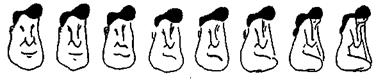
Рис. 5.7. Ефект гістерезису (з книги Г. Хакена "Синергетика").
Іншим цікавим прикладом подібної зміни точки зору є особливості процесу зорового сприйняття, що називаються ефектом гістерезису (рис. 5.7) та ефектом порушеної симетрії (рис. 5.8). В першому випадку зорове сприйняття об'єкта залежить від напрямку, в якому розглядається цей рисунок, тоді як в другому результат залежить від того, на чому фокусується увага - на центральній білій частині рисунка, де чітко видно вазу, або на бокових чорних частинах, де видно два обличчя.
Універсальні методи термодинаміки та синергетики можуть бути успішно застосовані і до вивчення політичних процесів, зокрема проблеми стійкості політичних систем.

Рис. 5.8. Ефект порушеної симетрії (з книги Г. Хакена "Синергетика").
Цікаві результати в цьому напрямку були отримані визначним українським фізиком і політичним діячем І. Р. Юхновським. Як вже вказувалося раніше, мірою впорядкованості будь-якої системи, в тому числі і політичної, є притаманна їй ентропія 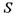 (або негентропія
(або негентропія 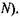 Чим менша величина ентропії
Чим менша величина ентропії 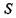 (або чим вище значення негентропії і
(або чим вище значення негентропії і 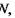 оскільки негентропія дорівнює ентропії з протилежним знаком:
оскільки негентропія дорівнює ентропії з протилежним знаком: 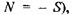 тим більш впорядкованою є система. Таким чином, переходу від менш досконалої до більш досконалої політичної системи відповідає зменшення ентропії або збільшення негентропії.
тим більш впорядкованою є система. Таким чином, переходу від менш досконалої до більш досконалої політичної системи відповідає зменшення ентропії або збільшення негентропії.
Стійкість будь-якої політичної системи визначається режимом її функціонування. І. Р. Юхновський пропонує розглянути такі два граничних режими функціонування політичних ситем:
1. Політична система є відкритою в термодинамічному розумінні цього терміну. Це означає, що система вільно обмінюється з навколишнім середовищем всім, чим можна обмінюватись - насамперед енергією, ентропією (негентропією) та інформацією.
Тут слід зауважити, що: а) ентропія й інформація визначаються однаковим чином; б) ентропія та інформація не можуть бути зведені до енергії.
Щоб краще зрозуміти останнє твердження, досить пригадати відомий приклад з киданням двох монет з однакової висоти. Нехай обидві монети однакові за інформацією, що в них міститься: на них, з одного боку, викарбований один і той самий герб, а на другому боці - однакова цифра. Проте вони мають зовсім різні маси. Тоді, коли ми їх одночасно кидаємо з однакової висоти, виділяється, звичайно, зовсім різна енергія, оскільки маси монет є різними (нагадаємо, що ця енергія дорівнює добутку маси на прискорення вільного падіння і на висоту). Що стосується інформації, яка отримується під час кидання цих монет, то вона є абсолютно однаковою і дорівнює 1 біту, оскільки реалізується один варіант з двох можливих (герб або цифра), тобто 0 або 1.
2. Політична система існує в режимі, ізольованому від зовнішнього середовища. Звичайно, не існує абсолютно ізольованих політичних і соціальних систем. Але є приклади, коли реальні системи існували в стані, який можна вважати досить наближеним до ізольованого стану (наприклад, колишній СРСР). Фізично стан подібної ізоляції відповідає адіабатичній ситуації, коли не відбувається теплообміну системи з навколишнім середовищем. Тоді, як випливає з першого закону термодинаміки (див. формулу (7.1)), будь-яка робота виконується за рахунок внутрішньої енергії системи. Це обов'язково призводить до зростання ентропії (чи зменшення негентропії), тобто до зменшення впорядкованого стану системи і, врешті-решт, до її деградації. Загальні перші принципи природи і суспільства, зокрема другий закон термодинаміки, дають змогу підтвердити цей важливий висновок щодо функціонування політичної системи, яка є ізольованою, а саме: абсолютно детермінований шлях до розпаду (тобто такий процес, який відбувається з ймовірністю, що дорівнює одиниці) є характерною рисою еволюції всіх ізольованих систем будь-якої природи.
Ще один дуже цікавий напрям досліджень, який має принципове значення для різних галузей знань і описує стрибкоподібні зміни поведінки систем різноманітної природи - це сучасна теорія катастроф. Розглянемо її основні принципи та ідеї.
У 1972 році в Нью-Йорку вийшла з друку давно анонсована до цього книга французького математика-тополога Р. Тома "Структурна стійкість і морфогенез". Вже сама назва цієї книги вказувала на її достатньо універсальний характер. Дійсно, Р. Том поставив перед собою задачу створення такого варіанта математичної теорії динамічних (еволюціонуючих) систем, який був би придатним для біології та інших галузей науки, досить далеких від математики і який в цьому сенсі не є настільки точним, як фізика, хімія і ряд інших наук. Основна ідея Р. Тома полягала в тому, щоб застосувати теорію динамічних систем з класифікацією особливих точок за А. Пуанкаре для аналізу як структурно-стійких станів, нечутливих до малих збурень (змін параметрів системи), так і різких (розривних) змін станів системи при плавній зміні параметрів, які називаються катастрофами.
По своїй суті знаходження особливих точок за методом А. Пуанкаре зводиться до відшукання стаціонарних, тобто тих, що не залежать від часу, розв'язків системи диференціальних рівнянь для параметрів порядку, які визначають поведінку досліджуваного об'єкта. Особливі точки знаходяться згідно з розв'язком відповідної системи диференціальних рівнянь стосовно так званих збурень по відношенню до стаціонарних розв'язків. Залежно від знака дійсної 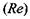 та уявної частини
та уявної частини 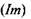 коренів
коренів 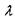 характеристичного рівняння особливі точки поділяються на стійкі та нестійкі вузли і фокуси, сідла та центри або граничні цикли (табл. 5.4).
характеристичного рівняння особливі точки поділяються на стійкі та нестійкі вузли і фокуси, сідла та центри або граничні цикли (табл. 5.4).
Рис. 5.9 ілюструє можливі види особливих точок для динамічних систем з двома параметрами порядку згідно з класифікацією А. Пуанкаре. Як бачимо з відповідних фазових портретів системи, для стійкого вузла характерний рух точки, що зображує динамічну еволюцію системи, до стаціонарного стану (особливої точки) як по першому, так і по другому параметру порядку. У разі нестійкого вузла система віддаляється від особливої точки по обох параметрах порядку. Якщо корені характеристичного рівняння мають різні знаки, тобто особлива точка - сідло, то така особлива точка є теж нестійкою, але лише по одному з параметрів порядку.
Таблиця 5.4. Типи особливих точок (класифікація Пуанкаре)
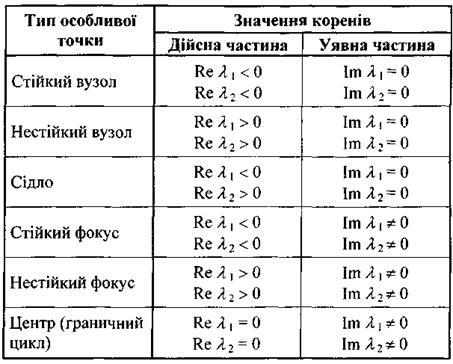
Якщо для стійкого і нестійкого вузлів та сідла характерна неперіодична поведінка, то для всіх інших особливих точок притаманна періодична (коливальна) поведінка динамічної системи. Для стійкого фокуса фазовий портрет зображується у вигляді спіралі, що накручується на особливу точку - це відповідає затухаючим коливанням в часі для обох параметрів порядку систем. Для нестійкого фокуса спостерігається зворотна ситуація - спіраль розкручується, що відповідає коливанням параметрів порядку, амплітуда яких зростає з часом. І нарешті, в останньому випадку центра (граничного циклу) в системі відбуваються незатухаючі коливання (автоколивання) параметрів порядку.
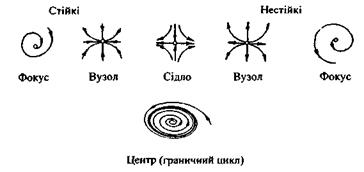
Рис. 5.9. Фазові портрети можливих видів особливих точок.
Зауважимо, що стійкі та нестійкі вузли та фокуси, а також сідла характеризують "грубі" системи, тоді як граничний цикл (центр) - "негрубі". Поняття "груба" і "негруба" системи були вперше введені завдяки дослідженням нелінійних динамічних систем, які були виконані визначним математиком О.О. Андроновим та його учнями. Під "грубою" системою мається на увазі така система, яка знаходиться поблизу свого рівноважного стану і яка не може бути виведена зі стану рівноваги при зміні параметрів. Очевидно, що "негруба" система легко виводиться за рахунок незначної зміни параметрів зі свого стану рівноваги, який є нестійким. Зрозуміло, що чисто математичне (точніше сказати - топологічне) поняття "грубості" і "негрубості" має надзвичайно широке застосування в психології, економіці, політиці та інших областях під час вивчення стійкості цих систем.
Повертаючись до теорії катастроф Р. Тома, можна сказати, що вона становить сучасний розвиток теорії стійкості динамічних систем А. М. Ляпунова (поняття стійкості взагалі є дуже важливою характеристикою динамічної системи) і теорії особливостей X. Уітні, які узагальнюють собою відомі в класичному математичному аналізі дослідження на екстремум. Недарма створення теорії катастроф порівнювалося в 70-х роках - роках її виникнення - з переворотом в математиці, пов'язаним зі створенням І. Ньютоном і Г.В. Лейбніцем диференціального і інтегрального числень.
Дослідження з нелінійної динаміки мали дуже великий вплив на формування основних ідей і принципів теорії катастроф. Так, значним результатом цих досліджень став суттєвий розвиток уявлень про біфуркації (термін "біфуркація" буквально означає "роздвоєння"), тобто про якісні перебудови динамічних систем.
Нові важливі результати в теорії біфуркацій належать визначному російському математику В. І. Арнольду, який незалежно від Р. Тома довів деякі принципові теореми в теорії катастроф. Р. Том, який вважається автором теорії катастроф, віддає пріоритет у винаході терміну "теорія катастроф" англійському математику - топологу К. Зіману. Саме К. Зіману присвятили свою прекрасну монографію "Теорія катастроф та її застосування" Т. Постон і І. Стюарт, написавши в передмові: "Кристоферу Зіману, біля ніг якого ми сидимо, на плечах якого ми стоїмо". Дивним є той факт, що математик К. Зіман придумав так звану "машину катастроф" - досить простий пристрій, який легко може бути виготовлений і який дає змогу дуже наочно спостерігати різкі зміни поведінки машини при незначній варіації параметрів. Опис "машини катастроф" можна знайти у чудовій, невеличкій за об'ємом книзі В. І. Арноль-да "Теорія катастроф", в якій подається, з одного боку, науково-популярне, а з іншого - дуже глибоке і витончене викладення основних принципів теорії катастроф.
Представляють інтерес висловлені В.І. Арнольдом загальні міркування з погляду теорії катастроф щодо тенденцій ("принципів") переходу до "кращого стану" системи довільної природи (фізичної, хімічної, біологічної, соціальної, політичної тощо).
1. "Принцип тендітності гарного (стійкого)": система, що знаходиться на границі стійкості, з більшою ймовірністю переходить в нестійкий стан. Це пов'язано з досить зрозумілим з інтуїтивного погляду правилом: "гарні" (зокрема, стійкі) системи повинні задовольняти кільком (інколи багатьом) вимогам, тоді як "погані" можуть мати хоча б один недолік, тобто між "гарними" і "поганими" системами в цьому сенсі відсутня симетрія.
2. "Принцип погіршення на шляху до кращого": в процесі послідовної еволюції системи до кращого стійкого стану з поганого нестійкого відбувається погіршення, до того ж на початковій стадії процесу переходу до кращого стану швидкість погіршення зростає. Максимум протидії на шляху до кращого реалізується до досягнення найгіршого стану. Далі в цьому самому поганому стані протидія зменшується і може повністю зникнути, коли система знаходиться вже достатньо близько до кращого стану.
3. "Принцип стрибкоподібного покращання": якщо система стрибком, а не в процесі поступової еволюції, проскакує найгірший стан і опиняється поблизу гарного, то далі вона самодовільно рухається в бік цього гарного стану.
4. "Принцип еволюції до катастрофи": нехтування основними законами природи і суспільства, які спираються на ефекти зворотного зв'язку (в суспільному житті та політиці - це, насамперед, особиста відповідальність за прийняті рішення), веде до катастрофи.
Таким чином, підводячи підсумок короткого огляду сучасних синергетичних процесів у природничих та суспільних науках, можна сказати, що значення синергетики для освіти і науки пов'язане з інтеграцією знань з різних дисциплін, посиленням міжпредметних зв'язків, використанням цього нового міждисциплінарного напряму для глибокого розуміння єдності законів природи і суспільства, а отже, розвитку особистості як кінцевої мети всієї освітянської діяльності.
Дата добавления: 2015-03-03; просмотров: 951;
