Стаціонарний стан відкритих систем і теорема Пригожина щодо мінімуму виробництва ентропії
Розглянемо поняття стаціонарного стану, котре відіграє важливу роль в термодинамічному описанні відкритих систем.
Повна зміна ентропії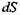 
у відкритій системі може бути представлена як сума двох доданків
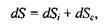(5.16)
що описують в загальному вигляді такі процеси:
1) процеси зміни ентропії всередині системи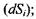 
2) процеси зміни ентропії через взаємодію відкритої системи з навколишнім середовищем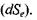 
Коли б всередині досліджуваної системи відбувалися лише зворотні процеси, то зміна ентропії була б відсутня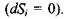 
Оскільки всередині реальної системи протікають незворотні дисипативні процеси, в результаті яких наробляється ентропія, то 
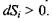Щодо знака величини 
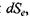то він може бути довільним і залежить від того, відбувається поступлення ентропії в систему або відтік ентропії з неї, пов'язаний з потоками частинок, тепла та іншими процесами переносу через поверхню, що обмежує виділений об'єм досліджуваної системи.
Стаціонарним називається такий стан системи, при якому ентропія всієї відкритої системи 5 зберігається, тобто повна зміна ентропії дорівнює нулю 
Із умови постійності ентропії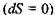 
і рівняння (5.16) безпосередньо випливає, що 
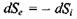. Тоді в силу позитивності зміни ентропії 
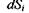за рахунок дисипативних процесів, що відбуваються всередині системи, зміна ентропії 
через взаємодію відкритої системи з довкіллям повинна бути від'ємною 
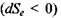і достеменно рівною за модулем зміні ентропії 
всередині системи. Подібна реалізація умови стаціонарності відкритої системи стає можливою, якщо ентропія, що наробляється всередині системи, повністю переходить в навколишнє середовище. Іншими словами, можна стверджувати, що відкриті системи у стаціонарному стані живляться негентропією (від'ємною ентропією) 
Пригожий довів, що у стаціонарному стані виробництво ентропії мінімальне 
Це твердження має назву "теорема Пригожина". Розглянемо міркування, що спонукають до встановлення цієї теореми.
Дійсно, з отриманих у параграфі 3.2.2 формул для виробництва ентропії 
та лінійного закону 
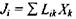маємо
(5.17)
Для спрощення обмежимося випадком двох термодинамічних сил і відповідно двох потоків. Тоді, беручи до уваги принцип симетрії кінетичних коефіцієнтів 
можна записати такий вираз для виробництва ентропії:
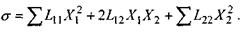
Обчислимо часткові похідні від виробництва ентропії а за термодинамічними силами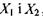 
, а саме:
Отже, коли в стаціонарному стані відкритої системи потоки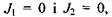 
то виробництво ентропії приймає екстремальне значення. В силу додатної визначеності квадратичної форми 
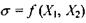і пов'язаної з цим позитивності других похідних
цей екстремум є мінімум (див. розділ 1 в першому томі), тобто виробництво ентропії у стаціонарному стані приймає мінімально можливе значення.
Принцип мінімуму виробництва ентропії у стаціонарному стані відкритої системи має надзвичайно важливе значення. Він дає кількісний критерій, що допомагає визначити напрямок розвитку (еволюції) відкритої системи будь-якої складності, а саме: якщо у відкритій системі відбуваються незворотні процеси поблизу термодинамічної рівноваги, то по зменшенню виробництва ентропії у такій системі можна передбачити її перехід у стаціонарний стан. Іншими словами, критерієм наближення системи до стаціонарного стану є від'ємність похідної від виробництва ентропії за часом, тобто виконання нерівності
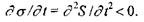(5.18)
Теорема Пригожина пояснює також принципову стійкість стаціонарних станів відкритих систем. Справді, якщо відкрита система самодовільно виходить з свого стаціонарного стану через флуктуації, то в ній відбувається збільшення швидкості виробництва ентропії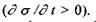 
Тоді через теорему Пригожина необхідним наслідком подібної зміни стану системи мають бути такі процеси всередині системи, при яких вона знову повернеться до свого початкового стаціонарного стану. Принцип мінімуму виробництва ентропії (теорема Пригожина) відіграє таку саму роль для відкритих систем, як принцип Ле Шательє-Брауна, що пояснює стійкість рівноважних систем: будь-який зовнішній вплив, який виводить систему з положення рівноваги, викликає в ній такі процеси, які прагнуть послабити результат цих зовнішніх впливів.
5.3. ВІДКРИТІ МЕДИКО-БЮЛОГІЧНІ СИСТЕМИ, ЩО ЗНАХОДЯТЬСЯ ДАЛЕКО ВІД РІВНОВАГИ (ЕЛЕМЕНТИ СИНЕРГЕТИКИ)
Визначним досягненням у розвитку науки за останні роки стало розуміння фундаментальних основ і принципів самоорганізації у відкритих системах різної природи (фізичних, хімічних, біологічних та ін.) поодаль від їх положення рівноваги. Зараз вже можна говорити про створення міждисциплінарної області науки - синергетики, котра вивчає загальні принципи самоорганізації і утворення просторових, часових і просторово-часових структур у відкритих нерівноважних системах. Сам факт утворення нових структур (упорядкування) в процесі еволюції знаходиться в уявному протиріччі з другим началом термодинаміки, з суті якого випливає, що з плином часу обов'язково відбувається зникнення структур (розупорядкування) з одночасним підвищенням сумарної ентропії всієї системи. Насправді цього протиріччя, що виникло ще при співставленні другого начала термодинаміки і еволюційного принципу Дарвіна, не існує. Утворення структур відбувається у відкритій підсистемі, котра завжди становить частину певної більшої системи. Якщо ця остання є замкненою системою, то дисипативні процеси, що у ній відбуваються, спонукають до зростання ентропії усієї системи, але це не обов'язково викликає зростання ентропії кожної її частини.
Поява наприкінці 80-х років XX століття нового міждисциплінарного наукового напряму, який отримав назву "синергетика", створила надійні засади для посилення інтеграційних тенденцій в науці та освіті. Як вже зазначалося, синергетика вивчає загальні принципи самоорганізації та утворення впорядкованих структур у відкритих нерівно-важних системах різної природи.
Термін "самоорганізація" визначає процеси (явища), які пов'язані із зміною структури і забезпеченням узгодженої поведінки системи завдяки наявності внутрішніх зв'язків і контактів із зовнішнім середовищем. Здатністю до самоорганізації і утворення впорядкованих структур володіють системи живої та неживої природи, а також штучні системи.
Якщо до виникнення синергетики природничі та інші науки могли обходитися під час використання системного підходу до своїх об'єктів дослідження без врахування колективних ефектів, які спонукають до утворення стійких структур в часі та просторі, нині послідовне вивчення цих проблем стало можливим на підставі синергетичних методів. Особливо важливим і гострим постає питання щодо впорядкованості і самоорганізації під час дослідження енергетичних, екологічних, соціальних, політичних, меди-ко-біологічних та інших глобальних проблем.
Існує досить велика кількість прикладів виникнення впорядкованих структур у системах різної природи:
у фізиці - це фазові переходи типу надпровідність і надплинність, конвективна нестійкість, стратти у газовому розряді, пентагональні структури у плазмі токамаків, когерентне випромінювання лазерів, солітони;
в астрофізиці - це червона пляма Юпітера, полярні сяйва;
у хімії - періодична окислювально-відновлювальна реакція Бєлоусова-Жаботинського;
у біології - періодичні процеси при гліколізі і фотосинтезі, морфогенетичні процеси у сімействі колективних амеб, коливальна динаміка чисельності популяцій;
у медицині - утворення ревербераторів (спіральних хвиль) у міокарді, спіральні хвилі і гексагональні структури у сітківці ока при депресії Леао;
в обчислювальній техніці - паралельні обчислення і надійність роботи ЕОМ, розпізнання образів;
у соціології і політології - формування суспільної думки, стійкість політичних систем;
в екології - поширення епідемій (пандемій) і забруднення, а також велика кількість інших процесів.
Просте перерахування цих прикладів показує, що синергетика тісно пов'язана з різними галузями науки і техніки. Це не означає, що вона використовує цілковито різнорідні поняття. Одним з головних аспектів світоглядного значення синергетики, ціннішим досягненням синергетичного підходу якраз і є те, що в ній вдається обгрунтувати нові "перші принципи", що лежать в основі процесів самоорганізації і впорядкування або, більш загально кажучи, функціонування відкритих складних систем.
Одна з основних причин процесів самоорганізації та впорядкування формулюється у вигляді принципу, який можна було б назвати "принципом узагальненого дарвінізму", а саме: просторові, часові та просторово-часові структури в органічному та неорганічному світі виникають як прояв колективних коливань через флуктуації, їх взаємодію і відбір тих з них, які мають найбільший час затухання (релаксації). Такі найтриваліші живучі процеси характеризуються змінними, які у синергетиці називаються параметрами порядку або керуючими модами (коливаннями). Саме вони визначають еволюцію системи, котра первісно мала дуже багато степенів свободи. В результаті колективної взаємодії різних мод у такій системі може виділитися лише кілька параметрів порядку. У цьому полягає зміст принципу підлеглості, котрий відіграє дуже важливу роль у синергетичних процесах.
Впорядковані структури, які утворюються у відкритих системах, далеких від рівноваги, поділяються на просторові, часові і просторово-часові (табл. 5.1).
До просторових структур відносяться гексагональні комірки Бенара, згадані вище спіральні структури, що в певний момент часу можна спостерігати в реакції Бєлоусова-Жаботинського (БЖ), в колонії соціальних амеб (плазмодії міксоміцети), в міокарді, на сітківці ока при депресії Лєао тощо.
Таблиця 5.1. Типи впорядкованих структур та їх параметри
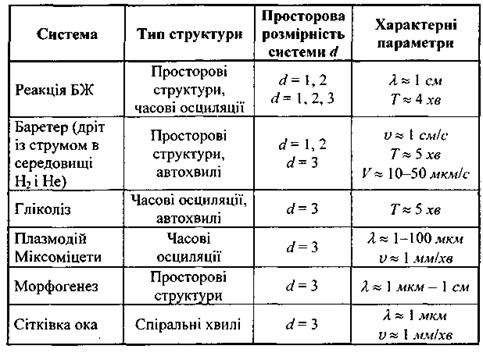
Часові структури спостерігаються в екологічних суспільствах (типовим прикладом є періодична з часом зміна чисельності популяцій в моделі "хижак-жертва", що буде розглянута пізніше), часові осциляції при гліколізі і фотосинтезі тощо.
Просторово-часові структури мають місце при спостереженні реакції Бєлоусова-Жаботинського протягом досить тривалого часу (десятки хвилин), в динамічних процесах розповсюдження ревербераторів в міокарді, при поширенні нервового імпульсу в аксоні тощо.
Розглянемо деякі приклади впорядкування та самоорганізації систем різної природи, про які згадувалося вище, докладніше. Особливу увагу при цьому ми будемо звертати на схожість, певну подібність цих явищ. Ця схожість поведінки різноманітних систем (наприклад, дивний перебіг періодичної хімічної реакції Бєлоусова-Жаботинського, утворення спіральних структур в колонії соціальних амеб, поява ревербераторів у міокарді тощо) дає підстави говорити про так званий "ізоморфізм", тобто подібність, явищ утворення впорядкованих структур у зовсім різних за своєю природою відкритих системах.
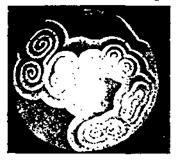
Рис. 5.1. Спіральні хвилі в реакції Бєлоусова-Жаботинського (фотографія А.Т. Вінфрі).
Періодична хімічна реакція Бєлоусова-Жаботинського. У 1951 році радянський хімік Б.П. Бєлоусов відкрив нову реакцію, суть якої зводилася до того, що протягом кількох годин з періодом приблизно 4 хвилини змінювався колір хімічно реагуючих компонентів - від червоного до синього і навпаки, тобто ця реакція бУла періодичною. Лише через вісім років Б.П. Бєлоусову вдалося надрукувати повідомлення про своє відкриття у реферативному журналі "Сборник рефератов по радиационной медицине" за 1958 г. Далі теоретичні аспекти цієї реакції розроблялися А.М. Жаботинським, а потім А.М. Заїкіним. Було з'ясовано, що хімічна реакція Бєлоусова є окисно-відновною, автокаталітичною реакцією, в якій беруть участь іони церія змінної валентності. Саме зміна валентності іонів церія від 3 до 4 (і навпаки) викликає зміну кольору реакції. У 1970 р. А.М. Заїкін і А.М. Жаботинський створили зручні умови для експериментального спостереження періодичної хімічної реакції, відкритої Б.П. Бєлоусовим, коли вилили розчин, в якому відбувалася ця реакція, тонким шаром в чашку Петрі. В такій системі, яка потім отримала назву хімічного реактора Заїкина-Жаботинського, ними спостерігалися спіральні автохвилі хімічної активності - дуже ефектні природні структурні утворення (рис. 5.1). Якщо спіральні хвилі в чашці Петрі, що вивчалися А.М. Жаботинським та А.М. Заїкіним, були двовимірні, то американський біофізик А. Уінфрі зміг спостерігати згодом тривимірні автохвилі хімічної активності. Детальний хімічний механізм періодичної реакції Бєлоусова був остаточно описаний (після перших робіт А.М. Жаботинського і А.М. Заїкіна) венгерським вченим Є. Керошем та американцями Р. Філдом і Р. Нойєсом. Останні розробили для цього спеціальну кінетичну модель, яка отримала назву "орегонатор" (за назвою американського штату Орегон, де мешкали автори цієї моделі). Інша кінетична модель "брюсселятор", що мала також за мету пояснення перебігу періодичної авто-каталітичної хімічної реакції Бєлоусова-Жаботинського, була створена І.Р. Пригожиним та Г. Ніколісом (назва моделі пов'язана, очевидно, зі столицею Бельгії, де у Вільному Університеті Брюсселя працює лауреат Нобелівської премії І.Р. Пригожий).
Спіральні структури в колонії соціальних амеб. Ще один дивний приклад самоорганізації можна спостерігати у біологічному суспільстві, а саме - в колонії соціальних амеб (грибів-слизовиків). Соціальними ці амеби називаються тому, що їм притаманна властивість до об'єднання (агрегації) у відповідні просторові структури, які мають спіральну форму. Виявляється, що коли амеби мають вдосталь їжі, вони існують як окремі і розвиваються індивідуально. Зовсім інша ситуація відбувається, коли їжа закінчується. Тоді голодні амеби починають спонтанно та в імпульсному режимі виділяти спеціальну хімічну речовину - цАМФ (циклічний аденозинмонофосфат), який відіграє роль морфогена, тобто сприяє формоутворенню. Просторовий розподіл цього морфогена, точніше кажучи, - градієнт концентрації цАМФ, є просторовою міткою, яка дає можливість всім іншим амебам збиратися (агрегувати) у спіральні або концентричні структури. Таким чином, механізм хімічної сигналізації виявився надзвичайно важливим у процесі формоутворення - морфогенезу. Принциповим є той факт, що структури в колонії соціальних амеб (рис. 5.2) виявляються подібними до автохвиль хімічної активності в реакції Бєлоусова-Жаботинського не лише за зовнішніми ознаками, а й тому що ці спіральні утворення виникають у відкритих системах, які є активними за своєю природою, (іншими словами, збудливими через існуючий в них запас енергії).
Рис. 5.2. Спіральні структури в колонії соціальних амеб (фотографія Г. Гереша і Б. Хесса).
Дата добавления: 2015-03-03; просмотров: 2829;