Пример 1. Построить приближенную развертку боковой поверхности конуса Ф, заданного окружностью k и вершиной S (рис

Построить приближенную развертку боковой поверхности конуса Ф, заданного окружностью k и вершиной S (рис. 181).

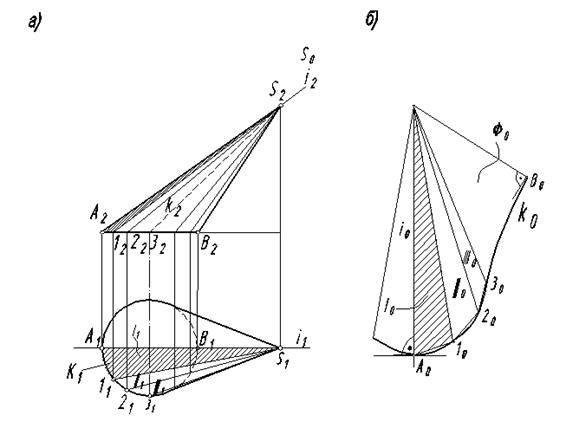
Заменим поверхность конуса поверхностью пирамиды, вписанной в конус. Чем больше сторон в основании будет иметь пирамида, тем точнее будет развертка конуса. За основание пирамиды примем правильный двенадцатиугольник. Так как заданная поверхность Ф имеет плоскость симметрии, то и развертка будет иметь ось симметрии. На рис.181б выполнена только половина развертки – до оси симметрии S₀A₀.

Для построения приближенной развертки конуса выполняем следующие построения:

1. Выбираем произвольную точку S₀, проводим вертикальную прямую l₀ и откладываем S₀A₀=AS, т.к. ребро AS||П₂,тоS₂A₂=AS. Используем метод триангуляции.

2. На ребре A₀ S₀достраиваем треугольник I₀со сторонами S₀1₀ и S₀A₀. Натуральная величина стороны A₁представлена на плоскости П₁ (A₁1₁=A₀1₀ – хорда, заменяющая дугу окружности).

Для определения натуральных величин боковых ребер пирамиды, они же являются обра-

зующими конической поверхности, необходимо использовать вспомогательные построения аналогичные тем, что были приведены на рис.179.

3. На развертке последовательно пристраиваем треугольники II₀, III₀…, которые соответствуют граням пирамиды II, III и т.д.

4. Полученную ломаную линию A_о1_о2_о3_оВ_о заменяем плавной кривой линией. Таким образом, мы построили приближенную развертку заданной конической поверхности.