Плоскости, касательные к поверхности

Плоскость, касательная к поверхности, имеет общую с этой поверхностью точку, прямую или плоскую кривую линию. Плоскость в одном месте может касаться поверхности, а в другом пересекать эту же поверхность.

Пусть задана некоторая поверхность W (рис. 185).

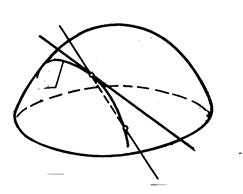
K t W l L a Рис. 185

Выберем на ней произвольную точку К и через нее проведем секущую прямую (а), которая пересечет заданную поверхность еще в некоторой точке L. Теперь точку L будем неограниченно приближать к точке К. При этом точка L будет перемещаться по некоторой кривой l, принадлежащей заданной поверхности. В пределе, когда точка L совпадет с точкой К, секущая (а) займет положение касательной t к кривой линии l и, следовательно, к поверхности Q в точке К. Таким образом, касательная к поверхности представляет собой предельное положение секущей, когда две точки проницания совпадут.

Из изложенного следует, что для построения касательной к поверхности в некоторой ее точке необходимо через эту точку провести принадлежащую поверхности кривую и построить касательную к этой кривой. Но через каждую точку поверхности можно провести множество кривых. Следовательно, через нее можно провести и множество касательных. В некоторых случаях все эти касательные принадлежат одной и той же плоскости, которую принято называть касательной плоскостью, в других случаях касательные принадлежат различным плоскостям (например, в точках ребра возврата поверхности торса вершин конических поверхностей, осей поверхностей вращения, где меридиан и ось пересекаются не под прямым углом и др.). В зависимости от этого, точки поверхности делятся на две группы: обыкновенные и особенные. В свою очередь, обыкновенные точки, в зависимости от характера заданной поверхности, делят на три типа: эллиптические, параболические и гиперболические.

К эллиптическимотносят такие точки, когда касательная плоскость имеет с поверхностью одну общую точку и все линии поверхности, проходящие через эту точку, будут находиться по одну сторону касательной плоскости. Поверхности, у которых все точки эллиптические, являются выпуклыми поверхностями, например, сфера, эллипсоид вращения, параболоид вращения и т.д.

Параболическиеточки составляют линию, по которой плоскость касается поверхности. Чаще всех такой линией является образующая поверхности. К поверхностям, содержащим параболические точки, относятся, например, линейчатые поверхности с одной направляющей (торсовые, цилиндрические и конические).

К гиперболическимотносятся такие точки, в которых касательная плоскость пересекает поверхность. К поверхностям, содержащим гиперболическиеточки, можно отнести, например, кольцо, однополостный гиперболоид, глобоид и др.

Следует заметить, что некоторые поверхности могут содержать различные точки. Например, на поверхности тора (кольца) есть эллиптические и гиперболические точки.

Поскольку для задания плоскости достаточно задать две пересекающиеся прямые, то для задания касательной плоскости некоторой точке поверхности достаточно провести через эту точку две касательные прямые (рис. 186).