Аксонометрические поверхности
На практике часто возникает необходимость в наглядном изображении предмета на чертеже. Это достигается построением аксонометрических проекций, сущность которых заключается в том, что изображаемый предмет располагается по отношению к некоторой плоскости проекций так, что при параллельном проецировании на нее ни одна из осей координат, к которым он отнесен в пространстве, не проецируется на плоскость проекций в виде точки. В результате ни одно из измерений изображаемого предмета не исчезает, и он проецируется на плоскость проекций в трех измерениях, а не в двух, как это получается при прямоугольном параллельном проецировании на три взаимно перпендикулярные плоскости проекций (рис. 198).
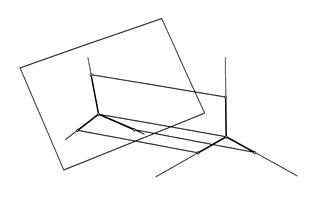
Рис. 198
|
Из рис. 198, на котором показано проецирование координатной системы на некоторую аксонометрическую плоскость проекций Р, видно, что в общем случае проекции равных между собой отрезков осей (АО = ВО = СО) не равны самим отрезкам и не равны между собой. Следовательно, размеры изображаемого предмета при аксонометрическом представлении по всем трем осям искажаются.
Величины 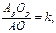
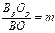 ,
, 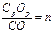 называются показателями (коэффициентами) искажения.
называются показателями (коэффициентами) искажения.
В зависимости от расположения плоскости проекций и направления проецирования возможны случаи, когда показатели искажения по всем трем осям одинаковы, или равны между собой только по двум осям, или показатели искажения по всем трем осям не равны между собой. Соответственно этому аксонометрические проекции называют изометрическими (изо – одинаковый), диметрическими (ди-двойной) и триметрическими.
Аксонометрические проекции бывают также прямоугольные (когда направление проецирования составляет с плоскостью проекций прямой угол) и косоугольные.
Для косоугольного проецирования показатели искажения и угол наклона a проецирующих лучей к плоскости проекций находятся в следующей зависимости:
k2 + m2 + n2 = 2 + ctg a
Для прямоугольного проецирования:
k2 + m2 + n2 = 2
Кроме этого, в обоих случаях сумма квадратов двух любых показателей искажения не может быть меньше единицы.
Дата добавления: 2015-02-25; просмотров: 1785;

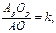
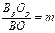 ,
, 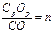 называются показателями (коэффициентами) искажения.
называются показателями (коэффициентами) искажения.