Плоскости, касательные к поверхностям вращения

Плоскость S, касательная к поверхности вращения в заданной на ней точке А, определяется двумя прямыми t, касательными к любым двум кривым линиям поверхности, проходящим через заданную точку. За такие линии обычно принимают параллель и меридиан поверхности вращения (рис. 187).

На рис. 188 на эпюре Монжа показаны построения касательной плоскости к поверхности вращения в заданной точке К на поверхности.

Наиболее целесообразно эту плоскость задать ее главными линиями (горизонталью h и фронталью f), проходящими через точку K. Фронтальная проекция h₂ горизонтали h будет проходить через точку К₂ параллельно экватору сферы. Для определения положения горизонтальной проекции h₁ горизонтали h через точку К проведем горизонтальную секущую плоскость уровня Г. При пересечении сферы этой плоскостью получим параллель l¹. Поскольку горизонталь h должна касаться этой параллели в точке К, то ее горизонтальная проекция h₁ должна касаться окружности l'₁ в точке К₁, в которую проецируется параллель l¹ на горизонтальную плоскость проекций П₁. Аналогично проведем фронталь f касательной плоскости.

На рис. 189 показаны построения касательной плоскости к поверхности вращения общего вида. Касательная плоскость определяется касательной прямой а к параллели точки К и касательной прямой b к меридиану этой точки.

Для определения фронтальной проекции В₂ касательной прямой меридиональную плоскость Г путем вращения ее вокруг оси i поверхности совмещаем с фронтальной меридиональной плоскостью. Касательная b занимает положение `b, в котором определяется точка S пересечения ее с осью i поверхности вращения.

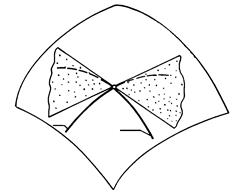
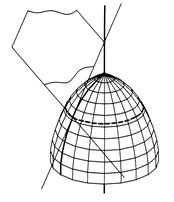
Рис. 186 Рис. 187

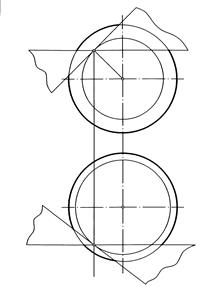
Рис. 188 Рис.189

При восстановлении плоскости Г точка S не меняет своего положения и, следовательно, искомой фронтальной проекцией касательной является прямая линия b₂. Плоскость, заданная двумя пересекающимися в точке К касательными а и b, является касательной плоскостью к заданной поверхности вращения в точке К. Плоскость, касательная к поверхности вращения в данной на ней точке, перпендикулярна меридиональной плоскости, проходящей через эту точку.

Касательные прямые к меридиональным кривым в точках одной и той же параллели являются образующими соприкасающегося по этой параллели конуса вращения с вершиной S на оси поверхности вращения. Плоскость, касательная к торсу, касается этой поверхности по ее прямолинейной образующей. На рис. 190 построена касательная плоскость в точке А к цилиндру.

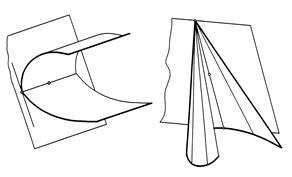
Рис. 190Рис. 191

Здесь касательная плоскость S определена образующей цилиндра, проходящей через точку А и касательной к направляющей линии а в точке 1 пересечения образующей с направляющей линией.

На рис. 191 построена касательная плоскость в точке А к конусу. Касательная плоскость определена образующей SA, проходящей через точку А, и касательной к направляющей линии а конуса в точке 1 пересечения образующей с направляющей линией.

На рис. 192 на эпюре Монжа показано построение плоскости, касательной к поверхности конуса в точке К. Наиболее целесообразно эту плоскость задать образующей а, проходящей через точку К, и горизонталью плоскости h.

Построение касательной плоскости к конической поверхности, проходящей через точку Е, расположенную вне поверхности, показано на рис. 193.

Через данную точку Е и вершину S конуса проведена прямая SE и определена точка К пересечения ее с плоскостью П направляющей линии конуса. Из точки К проведены касательные К₁ и К₂ к направляющей линии и через полученные точки касания проведены образующие S₁ и S₂. Плоскости SК₁ и SК₂, проходящие через данную точку Е, являются касательными плоскостями к конусу.

Построение касательной плоскости к цилиндру, проходящей через данную точку Е, когда точка Е лежит вне поверхности цилиндра, показано на рис. 195.

Цилиндр задан направляющей плоскостью кривой линией а и прямолинейной образующей g. Через точку Е проведена прямая линия ЕК, параллельная направлению образующих цилиндра, и определена точка К ее пересечения с плоскостью П направляющей линии. Из точки К проведены касательные К₁ и К₂ к направляющей линии, а через точки касания 1 и 2 – образующие цилиндра. Плоскости ЕК₁ и ЕК₂ являются касательными плоскостями к заданной цилиндрической поверхности. Схема построения плоскости, касательной к цилиндру и параллельной заданной прямой b, показана на рис. 195.

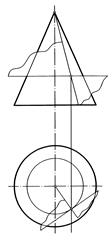
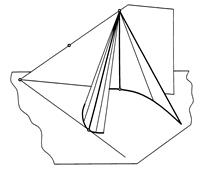
Рис. 192Рис. 193

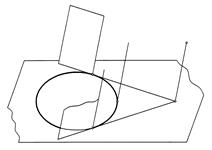
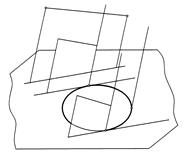
Рис. 194рис. 195

Цилиндр задан направляющей плоскости кривой линией а и прямолинейной образующей g. Через заданную прямую b проводим вспомогательную плоскость-посредник, параллельную образующим цилиндра. К направляющей линии цилиндра проводим касательную прямую, параллельную следу плоскости-посредника, а через точку касания (1 или 2) проводим образующую цилиндра. Касательная к направляющей и образующая определяют плоскость, касательную к заданной поверхности. Нормалью к поверхности в заданной точке называют прямую, перпендикулярную касательной плоскости к поверхности в рассматриваемой точке (рис. 196).

Построить нормаль к поверхности в некоторой ее точке означает построить нормаль к плоскости, касательной к поверхности в рассматриваемой точке.

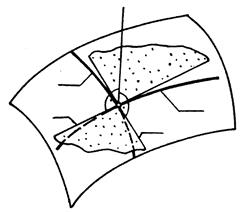
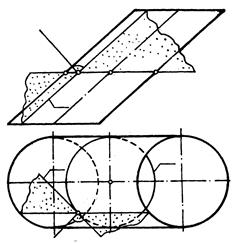
Рис. 196Рис. 197

Из этого следует, что поверхность имеет нормаль только в обыкновенных точках. Рассмотрим построение нормали к цилиндрической поверхности в точке К (рис. 197).

Построим плоскость, касательную к поверхности цилиндра в точке К. Эту плоскость целесообразно задать образующей а (которая одновременно является фронталью плоскости Qигоризонталью касательной плоскости h ). Построим нормаль к плоскости Q в точке К.

Вопросы для самопроверки

1. Какую плоскость называют касательной плоскостью к поверхности в данной точке?

2. Что называют нормалью поверхности в данной точке?

3. Какие точки поверхности называют эллиптическими, параболическими, гиперболи-

ческими?

4. Приведите примеры поверхностей, имеющих эллиптические, параболические или

гиперболические точки.