Способ раскатки

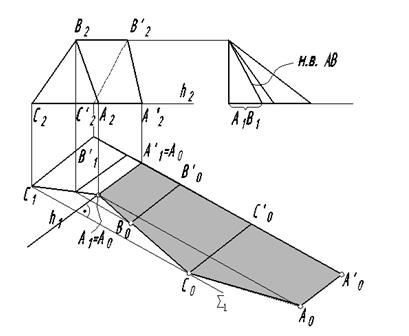
Пример 3. Построить развертку трехгранной призмы способом раскатки (рис.178).

Из рис.178 видно, что одна грань призмы AA ¢СС¢ параллельна плоскости П₁,либо лежит на ней. Будем поворачивать последовательно грани призмы вокруг ее боковых ребер до совмещения всех ее граней с плоскостью П₁ .При этом получим развертку боковой поверхности призмы.

Из условия задачи видно, что ребра призмы параллельны плоскости проекций П₁ , т.е. являются горизонталями. Вращаем грани призмы последовательно вокруг прямых A₀A₀ ¢ , B₀B₀ ¢,C₀C₀ ¢. При этом точки A,B,C будут перемещаться в плоскостях, перпендикулярных боковым ребрам, например, точка C Î S ^h. Чтобы построить развертку призмы , необходимо определить натуральную величину сторон AB, BC, CA. Для этого мы используем метод прямоугольного треугольника, рассмотренный ранее. Определив натуральную величину отрезка AB, найдем положение точки B₀. Выполняя аналогичные построения найдем точки C₀ и A₀.Точки A ¢,B ¢,C ¢, в данном случае перемещаются в одной плоскости, так как основание призмы A ¢B ¢ C ¢ ^AA¢^ h. Положение на развертке точек B₀ ¢, C₀ ¢, A₀¢определяется после построения точек A₀ ,B₀ ,C₀ .

В рассмотренных выше случаях построение разверток упрощалось, так как ребра призмы занимали частное положение относительно плоскостей проекций (||П₂ или ||П₁). Если по условию задачи ребра призмы будут занимать общее положение, необходимо вначале преобразовать чертеж так, чтобы ребра призмы заняли частное положение, а затем выполнять построение, аналогичные одному из описанных выше способов.