Пересечение конуса плоскостью
При пересечении кругового конуса, в зависимости от положения секущей плоскости, могут получиться следующие линии пересечения:
окружность, если секущая плоскость Г перпендикулярна к оси вращения конуса (рис.159,а);
эллипс, если секущая плоскость S пересекает все образующие конуса (рис.159,б);
гипербола, если секущая плоскость Р параллельна двум образующим конуса (рис.159,д);
парабола, если секущая плоскость Т параллельна одной образующей конуса (рис.159,в);
прямые линии, если секущая плоскость Q проходит через вершину конуса (рис.159,г);
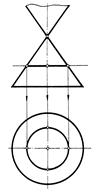
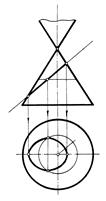
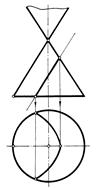
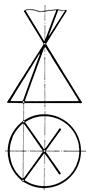
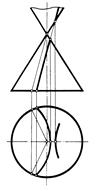
Рис. 159
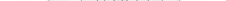
Проекции линии пересечения конуса плоскостью строятся по отдельным точкам.
Пример 1. Построить линию пересечения прямого кругового конуса фронтально проецирующей плоскостью Q (рис. 160).
На фронтальной проекции выделяем опорные точки 1 (12) и 2 (22), которые принадлежат очерковым образующим конуса, находим их горизонтальные проекции: 11, 21. Выбираем произвольные точки 3 º 3¢ (32º32¢), 4º4¢ (42º42¢), 5º5¢ (52º52¢). Проводим через вершину конуса и выбранные точки образующие на фронтальной проекции, строя горизонтальные проекции этих образующих, мы определяем и горизонтальные проекции этих точек. После этого все горизонтальные проекции точек соединяем плавной кривой линией. Полученное сечение представляет собой эллипс.
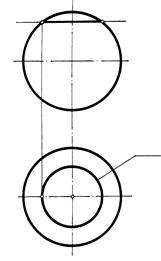
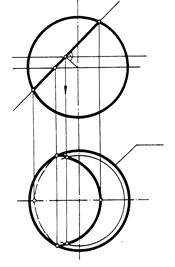
Рис. 161
Дата добавления: 2015-02-25; просмотров: 1285;
