Пример 3. По заданной фронтальной l2 построить недостающие проекции линии l, принадлежащей поверхности прямого кругового цилиндра (рис
По заданной фронтальной l2 построить недостающие проекции линии l, принадлежащей поверхности прямого кругового цилиндра (рис. 157).
В качестве опорных точек примем точки А и Е – начала и конца заданной линии, а также точку С, расположенную на пересечении линии l с профильным меридианом. В качестве вспо-могательных примем точки В и D, расположенные примерно посредине между каждой парой опорных точек.
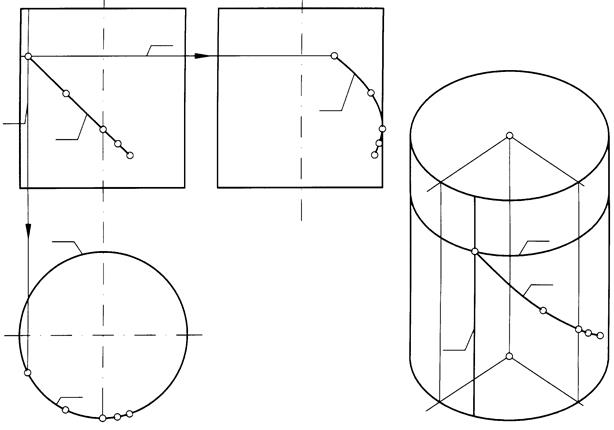
Рис. 157
Как и конус, цилиндр можно рассматривать и как поверхность вращения, и как линейную поверхность. Поэтому порядок определения горизонтальных проекций точек, принадлежащих поверхности цилиндра, по их фронтальным проекциям ничем принципиально не отличается от рассмотренного выше.
Горизонтальной границей видимости является линия верхнего основания цилиндра, поэтому вся горизонтальная проекция l1 линии l, будет невидимой.
Профильная проекция l3 линии l строится общепринятым способом. Ее часть А3В3С3 будет видимой, а вторая часть C3D3E3 – невидимой.
Контрольные вопросы
1. Укажите основные способы задания поверхности.
2. Что называют каркасом поверхности?
3. Что такое определитель поверхности?
4. Назовите основные виды перемещения производящей линии.
5. Как образуются и задаются на чертеже торсовые поверхности, поверхности вращения, винтовые поверхности?
6. Каковы основные свойства поверхности вращения?
7. Какие винтовые поверхности называют геликоидами?
8. Перечислите известные вам поверхности Каталана?
9. Какие косые поверхности называют линейчатыми поверхностями с направляющей плоскостью?
10. Поверхности параллельного переноса общего вида.
Дата добавления: 2015-02-25; просмотров: 1499;

