Несбалансированность в транспортной задаче

Если сумма запасов превышает сумму заказов (излишек запасов) или, наоборот сумма запасов меньше, чем сумма заказов (дефицит запасов) необходимо сбалансировать задачу. В первом случае,

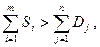
нужно добавить в таблицу транспортных издержек и в таблицу перевозок по одному лишнему столбцу.

Это можно трактовать так, как если бы появился еще один «фиктивный» потребитель. Если потребовать, чтобы заказ этого «потребителя» в точности равнялся бы разности между суммой всех запасов и суммой всех заказов

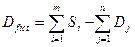
а издержки перевозок грузов к нему от любого поставщика равны нулю, будем иметь сбалансированную транспортную задачу. При этом переменные решения в последнем столбце дадут количество грузов, которые должны остаться на каждом из складов.

Во втором случае, когда

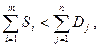
нужно добавить в таблицу транспортных издержек и в таблицу перевозок по одной лишней строчке. Это можно трактовать так, как если бы появился еще один «фиктивный» поставщик. Потребуем, чтобы запас этого «поставщика» в точности равнялся бы разности между суммой всех заказов и суммой всех запасов

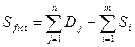
а издержки перевозок грузов от него к любому поставщику равны нулю. Вновь имеем сбалансированную транспортную задачу. При этом переменные решения в лишней строчке – это тот объем грузов, которые не получит каждый потребитель.

Заметим, что несбалансированные транспортные задачи можно, конечно, решать и просто заменив в соответствующих ограничениях знаки равенств на знаки нестрогих неравенств. Однако при этом надо иметь в виду, что для решения такой задачи MS-Excel будет применять общие методы решения ЛП- задач, а не специфические «транспортные» алгоритмы. В результате эффективность решения может быть значительно ниже, и получение целочисленного решения не гарантируется.

Еще одно возможное осложнение транспортной задачи – это запрещение определенной перевозки от i-го поставщика к j-му потребителю для составляемого плана перевозок (ремонт дороги, неплатеж и пр.). В этом случае, естественно, можно просто ввести ограничение x_ij =0. Однако, это вновь означает невозможность использования эффективных «транспортных» алгоритмов решения.

Чтобы сохранить форму транспортной задачи и учесть этот запрет, достаточно в таблице транспортных издержек заменить c_ij на очень большое число (на порядок большее, чем максимальная цена перевозки в таблице транспортных издержек). Это фактически будет означать, что оптимизационный алгоритм наверняка положит соответствующее значение перевозки x_ij равным нулю, поскольку перевозка по этому маршруту просто крайне невыгодна.

Подробнее о постановке и методах решения транспортной задачи можно узнать в [1, 3, 4].