Транспортные задачи. Теоретические основы

Классическая транспортная задача имеет целью минимизацию транспортных издержек при перевозках однотипных грузов от нескольких поставщиков (с различных складов), расположенных в разных местах, к нескольким потребителям. При этом в транспортной задаче, принимают в расчет только переменные транспортных издержек, т.е. считают, что суммарные издержки пропорциональны количеству перевезенных единиц груза. При постановке транспортной задачи необходимо прежде всего задать таблицу транспортных издержек для перевозок единицы груза 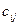от i-го поставщика к j-му потребителю. Эта таблица имеет m строк (по числу поставщиков) и n столбцов (по числу потребителей)

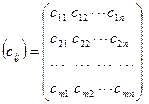
Таблица перевозок 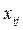имеет те же размеры ( 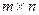) и содержит переменные решения.

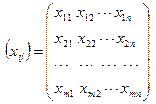
Необходимо также задать запасы поставщиков, готовые к вывозу

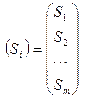
и величины заказов потребителей

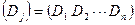
В транспортной задаче предполагается, что необходимо вывести запасы каждого i-го поставщика и удовлетворить заказ каждого j-го потребителя. Это возможно только если сумма запасов всех поставщиков равна сумме заказов всех потребителей.

Это важнейшее условие применимости эффективных алгоритмов.

Ограничения транспортной задачи имеют очень простой вид: сумма переменных решения вдоль каждой i-ой строки должна быть равна запасу поставщика S_i, а сумма переменных решения вдоль каждого j-го столбца должна быть равна заказу соответствующего потребителя D_j, переменные x_ij – не отрицательны.

Наконец, чтобы получить целевую функцию (суммарные издержки), необходимо рассмотреть суммы произведений каждой строки таблицы транспортных издержек на соответствующую строку таблицы перевозок и сложить их, суммируя по i от 1 до m. Это и даст двойную сумму. При этом номер источника (поставщика), 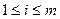, номер пункта назначения (потребителя), .

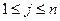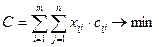
Если задача сбалансирована и никаких других ограничений, кроме упомянутых выше нет, Поиск решения использует эффективный алгоритм решения для этой задачи, причем, если запасы и заказы выражены целыми числами, то и переменные решения x_ij получатся целыми, даже если не требовать этого специально. Кроме того, гарантировано, что количество ненулевых перевозок x_ij не будет превышать m+n-1, т.е. количество «игроков» (поставщиков и потребителей) минус 1. Перечисленные выше соотношения представляют математическую модель транспортной задачи.