Цилиндрической передачи

Расчет геометрических параметров червячной цилиндрической передачи производится в соответствии с ГОСТ 19650-74. Модули и коэффициенты диаметра червяка этого типа передач регламентированы ГОСТ 19672-74.

В соответствии с ГОСТ 19036-81 исходный контур червячной цилиндрической передачи строится на основе следующих данных:

а) угол профиля принят равным 20°;

б) коэффициент высоты головки витка (зуба) h_a^* =1,0;

в) коэффициент высоты ножки витка (зуба) h_f^* = 1,2;

г) коэффициент радиального за­зора (зуба) с^* = 0,2.

В червячной передаче расчетным является осевой модуль червя­ка m_s, равный торцовому модулю червячного колеса. Он стандартизо­ван ГОСТ 2144-93.

Поскольку зубья червячного колеса нарезают червячными фрезами, то с целью сокращения номенклатуры инструмен­та принят и стандартизован коэффициент диаметра червяка: q = d₁ / m_S

(d₁ – делительный диаметр червяка).

Рекомендуется выбирать q = 0,25·z₂ (z₂ – число зубьев колеса). увеличение коэффициента диаметра червяка приводит к снижению КПД передачи, а уменьшение коэффициента “q” – к падению изгибной жесткости червя­ка. Поэтому минимально допустимым принято считать значение q_min= 0,212∙z₂ [4, с. 230].

Число зубьев колеса обычно находится в пределах от 30 до 300. Оптимальным для силовых передач принято назначать число зубьев колеса от 32 до 63 (не более 80). В редких случаях z₂ может достигать и 1000, например: в приводах мощных машин [4, с. 23I].

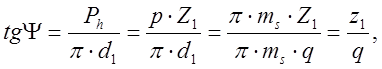Делительный угол подъема винтовой линии червяка можно рассчитать по формуле (рис. 8.6):

(8.1)

где z₁–число заходов червяка; регламентировано ГОСТ 2144-93 и

может быть равно 1, 2 или 4.

Р_h – ход резьбы, Р = р ^. Z₁ (Z₁ – число заходов резьбы);

р – шаг резьбы.

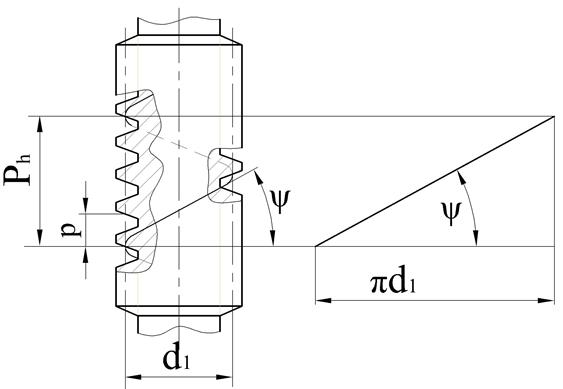
Рис. 8.6. Геометрические параметры цилиндрического червяка

Поскольку высота головки витка червяка (зуба колеса) равна h_a =h_a^* ·m_S = m_S, а высота ножки витка червяка (зуба колеса) равна

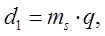
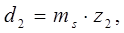h_f = h_f^* ·m_S =1,2·m_S , то делительные диаметры червяка d₁ и колеса d₂ определяют по зависимостям:

(8.2)

диаметры вершин d_ai и впадин d_fi червяка и колесасоответственно равны:

d_ai = d_i + 2h_a d_fi = d_i – 2h_f (8.3)

где i – порядковый номер элемента передачи; для червяка i =1и

для колеса i =2.

Наибольший диаметр колеса d_aM2 (см. рис. 8.2):

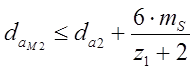(8.4)

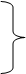
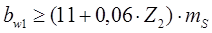Длину нарезанной части червяка вычисляют по эмпирическим зависимостям (см. рис. 8.2):

при Z₁ = 1 или 2; (8.5)

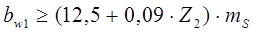
при Z₁= 4

Ширину венца червячного колеса рекомендуют принимать:

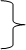b_w2 < 0,75 ·d_a1 при Z₁ = 1 и 2

b_w2 < 0,67 ·d_a1 при z₁ = 4 (8.6)

Центральный угол 2β , характеризующий полноту обхвата червяка венцом колеса, обычно принимают равным 2β = 90°…110°, в соответствии с приложением к ГОСТ 2144–93.

И наконец, межосевое расстояние передачи а_w стандартизо­вано ГОСТ 2144–93 в пределах от 40 до 500 мм (наиболее часто в машиностроении используют передачи с а_w = 63...100 мм).

Корригирование червячных передач выполняют в целях доведения межосевого расстояния до стандартного (или заданного) значения. По условию не подрезания и не заострения зубьев колеса значение коэффициен­та смещения исходного контура червяка выбирают в пределах –1 < x₁ < +1 [4, с.232].

В корригированных передачах геометрические параметры червяка и колеса вычисляют по формулам, приведенным в табл. 8.1

Таблица 8.1 – расчетные формулы для определения размеров червяка и колеса корригированной передачи

параметр	Червяк	Колесо
начальный диаметр
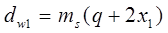
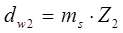
диаметр выступов
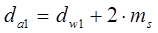
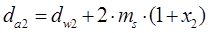
диаметр впадин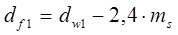

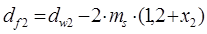
Примечание. 1. В стандартной червячной передаче корригируют только червяк. 2.Коэффициент коррекции червяка Х₁ выбирают по ГОСТ 2144-93, а коэффициент коррекции колеса Х₂ =0.

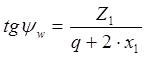Дополнительно для червяка рассчитывают угол подъёма витка на начальном цилиндре:

(8.7)