Напряжениям
Все расчеты червячной передачи можно разделить на три группы (табл. 8.3): расчеты червяка, расчеты червячного колеса и расчет передачи в целом.
Таблица 8.3 – Классификация расчетов червячной передачи
| Расчеты | ||
| передачи | червяка | колеса |
на нагрев:
 ,
где ,
где 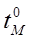 , , 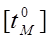 – фактическая и допустимая температура масла – фактическая и допустимая температура масла
| на изгибную жесткость: y < [y], где у, [y] – фактическая и допустимая стрелка прогиба оси червяка | на контактную прочность (проектный):
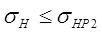 ,
где ,
где 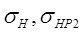 – фактическое и допускаемое контактные напряжения – фактическое и допускаемое контактные напряжения
|
| на усталостную прочность: s > [s], где s, [s] – фактический и допустимый (необходимый) коэффициент запаса прочности сечения вала | на изгибную прочность (проверочный):
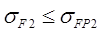 ,
где ,
где 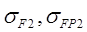 – фактические и допускаемые напряжения изгиба – фактические и допускаемые напряжения изгиба
|
Поскольку зубья колеса обладают меньшей прочностью и основная причина разрушения передачи – это заедание, то проектируют передачу по условию ограничения контактных напряжений:
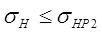 (8.11)
(8.11)
расчёт всех червячных передач по контактным напряжениям выполняют для зацепления в полюсе (аналогично зубчатым передачам), что позволяет:
Ø упростить расчётные зависимости и
Ø рассматривать зацепление в червяной паре как реечное косозубое.
В качестве исходной расчетной зависимости принимают известную формулу Герца–Беляева для наибольших контактных напряжений при сжатии цилиндров вдоль образующих. При этом зуб колеса рассматривают как цилиндр, а виток червяка как плоскость [4, с. 237]:
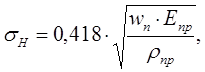
(8.12)
где ρпр – приведенный радиус кривизны соприкасающихся профилей;
Епр – приведённый модуль Юнга;
wn – нормальная нагрузка на единицу длины контактной линии.
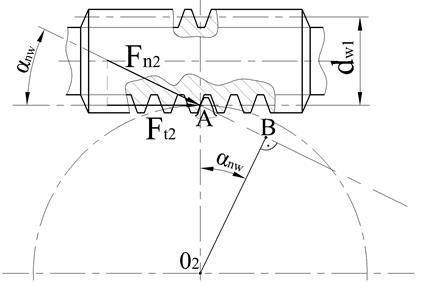
Рис. 8.10. К расчету цилиндрической червячной передачи
на выносливость по контактным напряжениям
В осевом (главном) сечении червяка виток Архимедова червяка имеет прямолинейный профиль. значит, радиус кривизны витка равен бесконечности: ρ1 = ∞.
Зубья колеса в этом сечении имеют эвольвентный профиль. Следовательно, приведенный радиус кривизны контактирующих профилей будет равен:
 (8.13)
(8.13)
В ф. (8.12) удельная нормальная нагрузка wn может быть определена по зависимости:
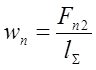
(8.14)
Здесь lΣ – суммарная длина контактных линий в зацеплении червячной передачи;
Fn2 – сила нормального давления на зуб колеса; её можно выразить через окружное усилие Ft2 .
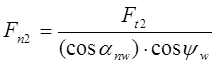 (8.15)
(8.15)
Длина одной контактной линии прямо пропорциональна начальному диаметру червяка dw1и углу обхвата 2.β (рис. 8.11).
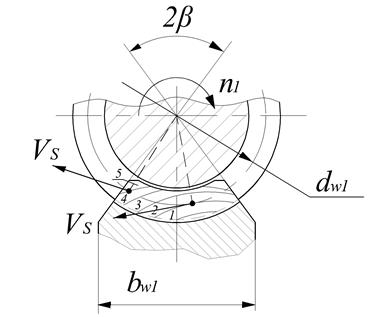
Рис. 8.11. Схема последовательного расположения (1…5)
контактной линии в процессе зацепления колеса
с архимедовым червяком
На величину суммарной длины контактных линий в зацеплении червячной передачи оказывают влияние геометрические и кинематические факторы [3, с. 225]:
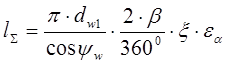 , (8.16)
, (8.16)
где ξ – коэффициент колебания суммарной длины контактных линий;
εα – коэффициент перекрытия.
При средних значениях коэффициентов ξ = 0,75 и εα = 2, при величине угла обхвата червяка колесом 2β = 1000 величина суммарной длины контактных линий 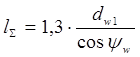 . Тогда ф. (8.14) примет вид:
. Тогда ф. (8.14) примет вид:
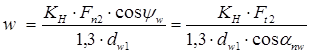 (8.17)
(8.17)
Здесь КН – расчетный коэффициент нагрузки; КН = КНβ. КНV = =1,1…1,4 [3, с. 213];
КНβ – коэффициент неравномерности распределения нагрузки в зоне контакта зубьев и витков из-за упругих деформаций деталей;
КНV – коэффициент неравномерности распределения нагрузки в зоне контакта вследствие внутренней динамичности передачи.
Если выразить окружное усилие через вращающий момент на колесе, то выражение (8.17) примет вид:

(8.18)
Тогда зависимость (8.12) примет вид:
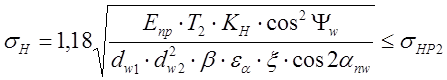
(8.19)
Преобразуем ф. (8.19), приняв следующий набор входящих в неё параметров [2, с. 214]:
αnw = 200; ψw=100; 2β = 1000 = 1,75рад; ξ = 0,75; εα =2; Е1=2,15.105 МПа (для стального червяка);
Е2 = 0,9.105 МПа (для бронзового колеса).
В результате преобразований получим формулу:
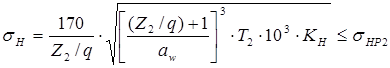 (8.19, а)
(8.19, а)
Если принять q =0,25. Z2, то ф. (8.20) будет преобразована в зависимость для проверочного расчета червячной передачи с Архимедовым червяком на контактную прочность:
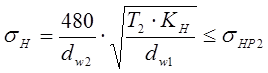 (8.20)
(8.20)
Качество проектирования передачи можно оценить путем вычисления относительного расхождения фактических и допускаемых контактных напряжений:
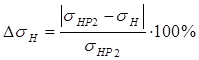 , (8.21)
, (8.21)
здесь sН– фактические контактные напряжения, вычисленные по
ф. (8.20);
sНP 2–допускаемые контактные напряжения материала колеса.
Если запас прочности зубьев колеса по контактным напряжениям не превышает 15…20% или перегрузка зубьев – не более 5%, то рассчитанные геометрические параметры передачи следует считать окончательными и не подвергать изменениям.
Если же запас прочности материала зубьев колеса по контактным напряжениям превысит 15%,то следует перейти либо к менее прочному материалу (из той же группы материалов), либо к предыдущему межосевому расстоянию и расчет повторить.
Ели перегрузка зубьев колеса по контактным напряжениям – более 5%, то необходимо перейти к более прочному материалу (из той же группы материалов), либо перейти к следующему стандартному межосевому расстоянию и расчет повторить.
Из условия (8.20) легко получить зависимость для проектного расчета червячной передачи (при том же наборе параметров):
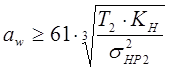 (8.22)
(8.22)
Полученное из расчета межосевое расстояние следует согласовать с ГОСТ 2144 – 93.
В расчетных зависимостях (8.20) и (8.22) приняты единицы измерения параметров: вращающий момент на колесе в Н.мм; диаметры и межосевое расстояние – в мм; контактные напряжения – в МПа.
Дата добавления: 2015-02-19; просмотров: 1082;
