Усеченное нормальное распределение.

Нормальное распределение предполагает, что случайная ве­личина может быть как положительной, так и отрицательной. Однако рассматриваемые здесь случайные величины могут быть только положительными, (например, прочность древесины на сжатие, собственный вес конструкций, величина площади опирания при со­пряжении конструкций крупноэлементных зданий). В этом случае можно использовать усеченное нормальное распределение (19.1).

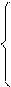
(19.1)

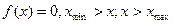
где х_min, x_max – предельные границы изменения случайной величины; с – нормирующий множитель

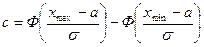
Если математическое ожидание много больше среднеквадра­тичного отклонения 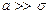, то можно принять обычные формулы нормального распределения. Практически вполне достаточно со­блюдение условия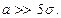

При анализе случайных величин, имеющих нормальное рас­пределение, часто приходится рассматривать вероятность односто­роннего выхода через некоторую границу. Для определения расчет­ных сопротивлений стали, бетона и древесины рассматривается нижняя граница (рис. 19.1) их случайных отклонений, ниже кото­рой конструкционные материалы не могут быть допущены к при­менению в несущих конструкциях. Для нагрузок устанавливается верхняя граница (рис.19.2) их случайных отклонений как наиболее опасная для строительных конструкций.

Вероятность того, что случайная величина окажется больше верхней границы, равна

(19.3)

Вероятность того, что случайная величина окажется меньше нижней границы, равна:

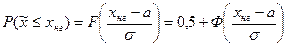(19.4)

Так как х_нг < а, то формулу (19.4) можно записать так:

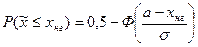(19.5)

Коэффициент вариации нормального распределения обычно значительно меньше 1/3, что на практике исключает возможность отрицательных значений для х.

Рис. 19.1. К определению вероятности повторения случайной величины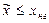

Рис. 19.2. К определению вероятности повторения случайной величины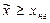

Лекция №10.