Применение нормального закона распределения для решения задач в строительстве.
Пример 20.1. Среднее квадратичное отклонение размера длины партии стеновых панелей σ = 10 мм. Определить вероятность того, что случайно взятая из партии панель:
1) отклонится от нормального (теоретического) размера на ±15 мм. По формуле (18.11) при  = 15 мм, а = 0 получим (рис. 20.1):
= 15 мм, а = 0 получим (рис. 20.1):
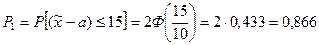
2) будет иметь превышение над номиналом от 5 до 25 мм. По формуле (18.10) имеем (рис. 20.2):
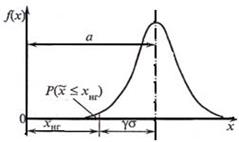
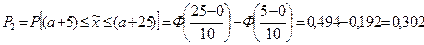 Пример 20.2. Стальной трос имеет среднюю несущую способность
Пример 20.2. Стальной трос имеет среднюю несущую способность  =500 кН, при которой напряжение в материале достигает предела прочности. Изменчивость прочности материала, из которого сделан трос, оценивается среднеквадратичным отклонением σ = 20 кН. Определить вероятность разрыва троса при нагрузке Q = 450 кН.
=500 кН, при которой напряжение в материале достигает предела прочности. Изменчивость прочности материала, из которого сделан трос, оценивается среднеквадратичным отклонением σ = 20 кН. Определить вероятность разрыва троса при нагрузке Q = 450 кН.
Имеем  =500 кН, нижняя граница случайной величины
=500 кН, нижняя граница случайной величины
хнг = 450 кН. Считая несущую способность троса случайной величиной, по формуле (19.3).
Найдем искомую вероятность (рис. 20.3).
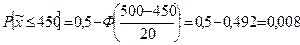
Пример 20.3. Нормированный резервный запас цемента в бункерах непрерывно действующего бетоносмесительного отделения составляет 10 т. По мере расходования этот запас регулярно пополняется. Однако в силу некоторых случайных причин среднеквадратичное отклонение запаса от среднего значения 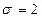 т. Определить вероятность того, что в данный момент времени запас цемента превышает 4 т или составляет
т. Определить вероятность того, что в данный момент времени запас цемента превышает 4 т или составляет
от 8 до 14 т.
Так как загрузка бункеров и расход цемента производятся малыми порциями и таким образом количество резервного цемента зависит от множества мелких случайных причин, можно предположить, что распределение количественной характеристики замеса цемента будет близким к нормальному.
Имеем а = 10т,  т, хнг = 14 т, х2 = 11 т, х1 = 8 т, по формуле (19.3) найдем вероятность (рис. 20.4)
т, хнг = 14 т, х2 = 11 т, х1 = 8 т, по формуле (19.3) найдем вероятность (рис. 20.4)
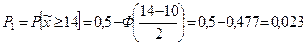
по формуле (18.10) найдем вероятность:
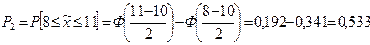
При определении Р2 учтено, что Ф(-1) = -Ф(1).
Пример 20.4. Номинальный срок службы здания составляет 50 лет. Среднеквадратичное отклонение срока службы от номинального равно 10 годам. Определить вероятность того, что здание прослужит от 60 до 70 лет или менее 40 лет.
Имеем: а = 50 лет, х2 = 70 лет, х1 = 60 лет, хнг = 40 лет.
По формуле (18.10) получим вероятность (рис. 20.5):
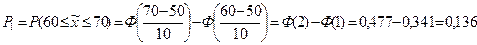 По формуле (18.10) получим вероятность:
По формуле (18.10) получим вероятность:
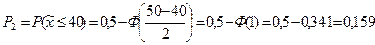
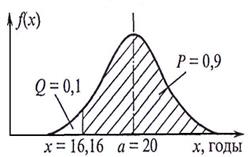
Пример 20.5. Срок службы шиферной кровли распределен по нормальному закону с параметрами: а = 20 лет,  года.
года.
Определить: 1) вероятность безотказной работы в течение 15 лет, 20 лет; 2) 90 %-й ресурс.
Продолжительность безотказной работы с определенной обеспеченностью называется ресурсом.
Вероятность безотказной работы кровли как события противоположное выходу ее из строя, равно
 (20.1)
(20.1)
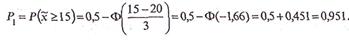 |
По формуле (20.1) найдем вероятность безотказной работы кровли t течение 15 лет (рис.20.6):
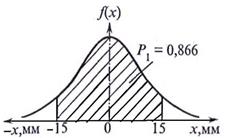
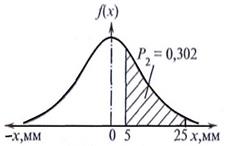
Рис.20.1. К определению Рис. 20.2. К определению
вероятности Р1. вероятности Р2.
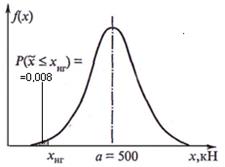

Рис. 20.3. К определению Рис. 20.4. К определению
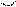 вероятности Р(х≤450) вероятности Р1 и Р2 в примере 20.3
вероятности Р(х≤450) вероятности Р1 и Р2 в примере 20.3
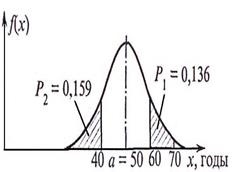
Рис.20.5. К определению Рис. 20.6. К определению
вероятностей срока службы Р1 и Р2 вероятности Р1.
Аналогично определяется вероятность безотказной работы кровли в течение 22 лет:
2) 90 %-му ресурсу соответствует вероятность отказа
Q = 1 - 0,9 = 0,1.
Так как Q = 0,1 < 0,5, то квантиль 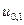 отрицательный. Из таблицы интеграла вероятностей найдем, что значение
отрицательный. Из таблицы интеграла вероятностей найдем, что значение
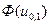 = 0,5 - Q = 0,4 соответствует квантилю
= 0,5 - Q = 0,4 соответствует квантилю 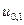 = 1,28. Это значение квантиля со знаком минус подставляем в равенство (18.8):
= 1,28. Это значение квантиля со знаком минус подставляем в равенство (18.8):
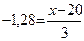 (20.2)
(20.2)
где х — искомое значение ресурса с 90 %-и обеспеченностью.
Из (20.2) найдем (рис. 20.7), что х = 20-3х1,28 = 16,16 лет.
Рис. 20.7. К определению 90 %-го ресурса шиферной кровли.
Дата добавления: 2015-02-16; просмотров: 1642;
