Основные положения вероятностного расчета строительных конструкций.

В настоящее время общепризнано, что поведение строительных конструкций в эксплуатации обусловлено взаимодействием целого ряда факторов случайной природы. Поэтому методы их расчета должны быть основаны на использовании вероятностных методов, отражающих смысл физических явлений. Академиком В.В. Болотиным сформулированы основные положения, которые должны лежать в основе современной теории расчета строительных конструкций.

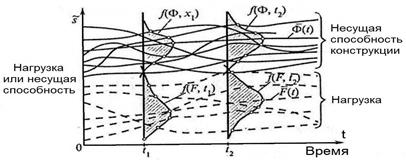
Первое положение состоит в том, что внешние воздействия на конструкцию и ее поведение в эксплуатации являются случайными процессами, развертывающимися во времени. Правильное решение проблемы надежности и долговечности связано с привлечением аппарата теории случайных функций. При расчете строительных конструкций наиболее часто в качестве аргумента случайной функции выступает время. Конкретный вид, принимаемый случайной функцией в результате опыта, представляет собой обычную детерминированную функцию, а в любой момент времени сечение семейства реализаций случайного процесса представляет собой плотность распределения случайной величины. Многие компоненты нагрузок и несущей способности по своей природе и изменению с течением времени (рис. 23.1) относятся к случайным процессам:

• ветровая нагрузка на здания и сооружения;
• крановая нагрузка;
• снеговая нагрузка и сейсмические воздействия;
• несущая способность железобетонной конструкции, не остающаяся постоянной в связи с изменением прочности бетона с течением времени;
• ползучесть бетона;
• коррозионные явления стальных элементов и арматуры в железобетонных конструкциях;
• деформативность древесины при воздействии длительных нагрузок.

Случайная функция имеет следующие вероятностные характеристики:

• плотность распределения в любой момент времени f(x,t);

математическое ожидание, являющееся функцией времени: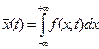

• дисперсия, характеризующая разброс случайной величины x в любой момент времени:

• корреляционная функция, описывающая связь между ординатами различных сечений случайного процесса:

K(t₁,t₁)= 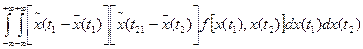(23.1)

где t₁ и t₂ – два любых частных значения аргумента t;

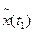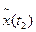и - случайные величины при частных значениях аргументов функций t₁ и t₂.

- совместная площадь распределения случайных величин в моменты t₁ и t₂.

При t₁ = t₂ = t корреляционная функция переходит в дисперсию.

Рис. 23.1. Случайный процесс нагружения и несущая способность конструкции.

Второе положение заключается в том, что надежность отождествляется с вероятностью нахождения параметров системы (конструкции, здания, сооружения) в допускаемой области, а нарушение надежности рассматривается как выход из этой области.

Для строительных конструкций такой выход равносилен прекращению их функционирования вследствие исчерпания несущей способности при воздействии статической или многократно повторной нагрузки, коррозии металла и бетона в результате агрессивного воздействия окружающей среды, возникновению недопустимых деформаций, колебаний, чрезмерному раскрытию трещин. Эта вероятность пребывания системы в допустимой области близка к единице.

Третье положение состоит в том, что отказы несущих конструкций наступают, как правило, в результате постепенного накапливания повреждений, остаточных деформаций, образования и развития трещин, коррозии металла и др.

Условие надежности строительной конструкции в течение времени ее эксплуатации имеет вид:

Р(t)>P_H (23.2)

где Р(t) – вероятность безотказной работы конструкции в любой момент времени;

Р_н – нормативное значение вероятности безотказной работы конструкции.

Левая часть неравенства (23.2) означает, что опасное состояние конструкций не наступает, если внутренние усилия от внешней погрузки F меньше несущей способности конструкций Ф:

Ф – F > 0 (23.3)

Требование абсолютного выполнения неравенства (23.3) лишено смысла, поскольку нагрузки и несущая способность носят случайный характер. Это требование может быть выполнено с вероятностью Р(t), близкой к единице.

Условие надежности (23.2) должно соблюдаться по всем возможным признакам выхода из строя несущей конструкции:

• исчерпание несущей способности;
• потеря местной и общей устойчивости;
• исчерпание прочности вследствие совместного воздействия нагрузки и неблагоприятного влияние окружающей среды;
• исчерпание ресурса выносливости стали и бетона от воздействия многократно повторных нагрузок;
• коррозия металла, в том числе арматуры в железобетонных конструкциях.

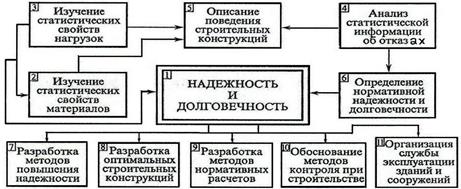
Общая структура схемы определения надежности строительных конструкций (рис. 23.2) предполагает решение задач, связанных с подготовкой представительной исходной информации, с обеспечением необходимого качества изготовления и монтажа, соблюдением нормированных режимов эксплуатации конструкций зданий и сооружений. Прежде всего необходимо накопить, проанализировать и подвергнуть статистической обработке информацию об изменчивых случайных факторах (материалах, нагрузках, геометрических размерах, условиях эксплуатации – см. информационные блоки 2,3 на рис. 23.2).

Построение распределений нагрузок и несущей способности по различным признакам, а также определение вероятности безотказной работы конструкций выполняется с применением методов теории вероятностей и теории надежности (теория случайных процессов, теория выборочных распределений).

Сбор и анализ статистической информации об отказах и последствиях этих отказов (информационный блок 4) позволяют выявить слабые места в конструкциях и решать задачу по определению нормативных вероятностей безотказной работы строительных конструкций (информационный блок 6) в соответствии с реальными условиями эксплуатации. В результате изучения экспериментальных данных о нагрузках, материалах, об отказах и их последствиях, использования теоретических разработок и поражений составляется модель поведения строительных конструкций в эксплуатации (информационный блок 5).

Результаты экспериментальных исследований и теоретических разработок, сосредоточенные в информационных блоках 2, 3, 4, 5, 6, являются основой для определения надежности и долговечности строительных конструкций (информационный блок 1) на всех стадиях ее функционирования, включая изготовление, монтаж и эксплуатацию.

Апробированный и подкрепленный представительными экспериментальными данными вероятностный метод расчета используется для обоснования разработки и выбора рациональных и оптимальных конструктивных решений строительных конструкций (информационный блок 8).

В результате вероятностной оптимизации искомых параметров конструкции в совокупности с детерминированными методами расчетов создается конкурентоспособная несущая конструкция, обладающая высокими эксплуатационными качествами, экономически выгодная и обладающая необходимыми запасами надежности и долговечности.

Расчетный аппарат теории надежности дает возможность обоснованно разрабатывать и осуществлять методы контроля качества при изготовлении и монтаже. Применение методов теории надежности позволяют выявить и реализовать дополнительные ресурсы несущей способности, в определенных условиях достичь снижения расхода материалов и получить экономический эффект при изготовлении и монтаже. Эти методы позволяют управлять качеством строительной продукции (информационные блоки 10, 11).

Условие надежности (23.2) является эффективным средством анализа технических норм и обоснованного назначения расчетных параметров нагрузок и материалов. Оно используется:

• для усовершенствования нормативных документов федерального и отраслевого применения (информационный блок 9);
• для решения различного рода задач по обеспечению надежности и долговечности при проектировании, изготовлении, монтаже и эксплуатации строительных конструкций;
• в расчетно-теоретических исследованиях.

Зная, причины отказов несущей конструкции как в процессе строительства, так в эксплуатации, следует их учитывать при проектировании новых конструкций и выполнении ремонтных работ и тем самым повышать надежность конструкции (информационный блок 7).

Рис.23.2. Общая структурная схема определения надежности строительных конструкций.