Определение нормативных сопротивлений материалов.

Определение нормативных сопротивлений материалов выполняется на основе опытных испытаний стандартных образцов. С этой целью определяются следующие величины, необходимые для определения нормативных сопротивлений:

- Среднее значение предела прочности (предел текучести)

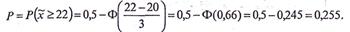
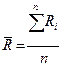(21.1)

R_i - значение случайной величины предела прочности или текучести

n - число опытов

- Средне-квадратичное отклонение

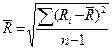(21.2)

- Коэффициент вариации

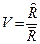(21.3)

Пример 21.1. Необходимо запроектировать экономичную конст­рукцию деревянной фермы. Для ее изго­товления имеется две партии древесины с различными вероятностными характе­ристиками временного сопротивления:

• партия № 1 — математическое ожидание временного сопротив­ления 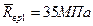, коэффици­ент вариации V₁= 0,25;

• партия № 2 — математическое ожидание 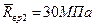коэффициент вариации V₂ = 0,15.

Считая закон распределения прочности древесины нормальным, опре­делить, из какой партии древесины можно запроектировать более экономич­ную ферму.

Нормативное сопротивление должно гарантироваться с обеспеченнос­тью Р = 0,95, и задача сводится к определению нижней границы случайной величины, выше которой вероятность повторения временного сопротивления равна 95 %.

В нашем случае нижняя граница случайной величины равна норматив­ному сопротивлению древесины R^H, т.е.

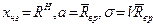(21.4)

(21.5)

Из равенства (21.5) с учетом обозначений (21.4) следует:

Так, как 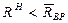, то квантиль и отрицательный. Из таблицы интеграла вероятностей найдем, что значению Ф(и) = 0,45 соответствует квантиль . Это значение квантиля со знаком минус подставляем в равенство (18.8) с учетом обозначений (21.4):

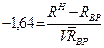(21.6)

Из (21.6) следует, что нормативное сопротивление древесины равно:

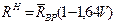(21.7)

Определяем нормативное сопротивление древесины по формуле (21.7):

· для партии № 1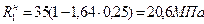

· для партии № 2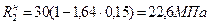

Нормативное сопротивление в партии № 2 больше, чем в партии

№ 1: (22,6 > 20,6).

Следовательно, более экономичной является ферма, запроектированная из партии № 2, так как с увеличением нормативного сопротивления расход материалов снижается. Следует обратить внимание, что, несмотря на более низкую среднюю прочность

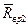= 30 МПа < 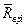= 35 МПа, нормативное сопротивление древесины в партии № 2 получилось большей величины за счет ее повышенной однородности (ее лучшего качества).

Кривые распределения прочности древесины в партиях № 1 и № 2 представлены на рис. 21.1.

Аналогично, по формуле (21.7) определяются нормативные сопротивления бетона, арматуры, стального проката и других материалов.

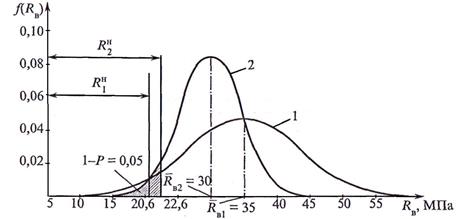
Рис. 21.1. Кривые распределения прочности древесины:

1 — для партии № 1; 2 — для партии №2.